

| A. | 36π | B. | 72π | C. | 144π | D. | 18π |
分析 作OC⊥AB,根据垂径定理得出AC=9米,继而可得圆的半径OA的值,再根据扇形面积公式可得答案.
解答 解:过点O作OC⊥AB于C点.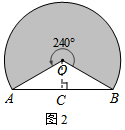
∵OC⊥AB,AB=18米,
∴AC=$\frac{1}{2}$AB=9米,
∵OA=OB,∠AOB=360°-240°=120°,
∴∠AOC=$\frac{1}{2}$∠AOB=60°.
在Rt△OAC中,OA2=OC2+AC2,
又∵OC=$\frac{1}{2}$OA,
∴r=OA=6$\sqrt{3}$.
∴S=$\frac{240}{360}$πr2=72π(m2).
故选:B.
点评 本题主要考查垂径定理和扇形的面积公式,熟练掌握垂径定理求得圆的半径是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,将一个长为10cm,宽为8cm的矩形纸片从下向上,从左到右对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的四边形的面积为( )
如图,将一个长为10cm,宽为8cm的矩形纸片从下向上,从左到右对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的四边形的面积为( )| A. | 10cm2 | B. | 20cm2 | C. | 40cm2 | D. | 80cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12.07×1010 | B. | 1.207×1011 | C. | 1.207×1012 | D. | 1.207×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
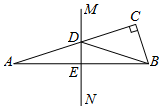 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A为( )
如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A为( )| A. | 18° | B. | 20° | C. | 22.5° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
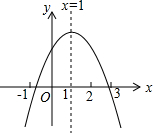 已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
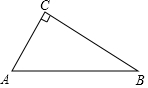 如图,在Rt△ACB中,∠C=90°,∠A=60°,AB=8.点P是AB边上的一个动点,过点P作PD⊥AB交直角边于点D,设AP为x,△APD的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,在Rt△ACB中,∠C=90°,∠A=60°,AB=8.点P是AB边上的一个动点,过点P作PD⊥AB交直角边于点D,设AP为x,△APD的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 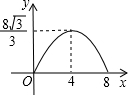 | B. | 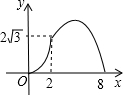 | C. | 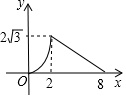 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ① | D. | ② |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
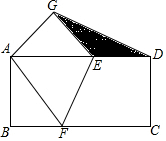 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )
如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )| A. | 5 | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com