按指定的方法解下列方程:
(1)2x2-5x-4=0(配方法);
(2)3(x-2)+x2-2x=0(因式分解法);
(3)(a2-b2)x2-4abx=a2-b2(a2≠b2)(公式法).
解:(1)∵2x
2-5x-4=0,
∴2x
2-5x=4,
∴x
2-

x=2,
∴x
2-

x+16

=2+

,
∴(x-

)
2=

,
解得:x
1=

,x
2=

;
(2)∵3(x-2)+x
2-2x=0,
∴3(x-2)+x(x-2)=0,
∴(x-2)(3+x)=0,
即x-2=0或3+x=0,
解得:x
1=2,x
2=-3;
(3)∵(a
2-b
2)x
2-4abx=a
2-b
2(a
2≠b
2),
∴(a
2-b
2)x
2-4abx-(a
2-b
2)=0,
∴a=a
2-b
2,b=-4ab,c=-(a
2-b
2)=b
2-a
2,
∴△=b
2-4ac=(-4ab)
2-4×(a
2-b
2)(b
2-a
2)=4(a
2+b
2)
2,
∴x=

=

,
解得:x
1=
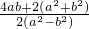
=

,x
2=-
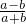
.
分析:(1)按要求,利用配方法求解即可求得求得答案;
(2)首先提取公因式(x-2),即可得到(x-2)(3+x)=0,继而求得答案;
(3)利用公式法,注意首先把原式化为一般式,然后求得判别式△的值,继而求得答案,注意分式的化简.
点评:此题考查了一元二次方程的解法.此题难度适中,注意要按要求求解是解此题的关键.

 x=2,
x=2, x+16
x+16 =2+
=2+ ,
, )2=
)2= ,
, ,x2=
,x2= ;
; =
= ,
,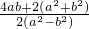 =
= ,x2=-
,x2=-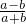 .
.

 阅读快车系列答案
阅读快车系列答案