
分析 (1)当每天进报纸是100份时,根据有20天每天可以卖出200份,其余的10天每天就只能卖出120份可知道报纸都能卖出,从而求得利润;
(2)当进150份报纸时,有10天卖出120份,所以有剩下的报纸,再根据当天卖不掉的报纸以每份0.10元退回给报社可求出利润;
(3)设每天从报社买进晚报x份(120≤x≤200)时,利润y=20天全卖掉情况的利润+10天卖掉120份的利润-10天中每天卖不掉的报纸赔的钱,根据此关系式可列出函数式.
解答 解:(1)一个月每天买进该晚报的份数为100时:30×(0.30-0.20)×100=300(元);
(2)一个月每天买进该晚报的份数为150时:20×(0.30-0.20)×150+10×(0.30-0.20)×120-10×(0.20-0.10)×(150-120)=390(元);
(3)设每天从报社买进晚报x份(120≤x≤200且为整数)时,
y=20(0.30-0.20)x+10×(0.30-0.20)×120-10(x-120)(0.20-0.10)=x+240.
当x取最大值时,y取到最大值.
x的最大值为200,
∴y=200+240=440.
月利润的最大值为440.
点评 本题考查一次函数的应用,根据题意列出函数式,以及根据函数式的特点和自变量的取值范围求出最值.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
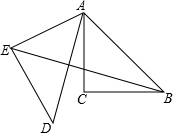 已知,在Rt△ABC中,∠C=90°,∠BAC=45°,AC=2,将△ABC绕点A顺时针旋转60°得到△ADE,连接BE,则BE的长为$\sqrt{2}+\sqrt{6}$.
已知,在Rt△ABC中,∠C=90°,∠BAC=45°,AC=2,将△ABC绕点A顺时针旋转60°得到△ADE,连接BE,则BE的长为$\sqrt{2}+\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com