
【题目】已知,在![]() 中,
中, ![]() .过A点的直线
.过A点的直线![]() 从与边
从与边![]() 重合的位置开始绕点
重合的位置开始绕点![]() 按顺时针方向旋转角
按顺时针方向旋转角![]() ,直线
,直线![]() 交BC边于点
交BC边于点![]() (点
(点![]() 不与点
不与点![]() 、点
、点![]() 重合),
重合),![]() 的边
的边![]() 始终在直线
始终在直线![]() 上(点
上(点![]() 在点
在点![]() 的上方),且
的上方),且![]() ,连接
,连接![]() 。
。
(1)当![]() 时,
时,
①如图a,当![]() 时,求
时,求![]() 的度数;
的度数;
②如图b,当![]() 时,
时, ![]() 的度数是否发生变化?说明理由.
的度数是否发生变化?说明理由.
(2)如图c,当![]() 时,请直接写出
时,请直接写出![]() 与
与![]() 之间的数量关系,不必证明.
之间的数量关系,不必证明.
![]()

【答案】(1)①∠ANC=45°;②当θ≠45°时,①中的结论不发生变化. 理由见解析
(2)∠ANC=90°﹣![]() ∠BAC.理由见解析
∠BAC.理由见解析
【解析】试题分析:(1)①证明四边形ABNC是正方形,根据正方形的对角线平分一组对角线即可求解;②根据等腰直角三角形的性质可得∠BNP=∠ACB,然后证明△BNP和△ACP相似,根据相似三角形对应边成比例可得![]() ,再根据两边对应成比例夹角相等可得△ABP和△CNP相似,然后根据相似三角形对应角相等可得∠ANC=∠ABC,从而得解;
,再根据两边对应成比例夹角相等可得△ABP和△CNP相似,然后根据相似三角形对应角相等可得∠ANC=∠ABC,从而得解;
(2)根据等腰三角形的两底角相等求出∠BNP=∠ACB,然后证明△BNP和△ACP相似,根据相似三角形对应边成比例可得![]() ,再根据两边对应成比例夹角相等可得△ABP和△CNP相似,然后根据相似三角形对应角相等可得∠ANC=∠ABC,然后根据三角形的内角和定理列式整理即可得解.
,再根据两边对应成比例夹角相等可得△ABP和△CNP相似,然后根据相似三角形对应角相等可得∠ANC=∠ABC,然后根据三角形的内角和定理列式整理即可得解.
试题解析:(1)①∵∠BAC=90°,θ=45°,
∴AP⊥BC,BP=CP(等腰三角形三线合一),
∴AP=BP(直角三角形斜边上的中线等于斜边的一半),
又∵∠MBN=90°,BM=BN,
∴AP=PN(等腰三角形三线合一),
∴AP=PN=BP=PC,且AN⊥BC,
∴四边形ABNC是正方形,
∴∠ANC=45°;
②连接CN,
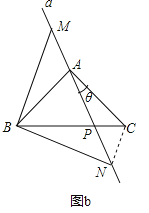
当θ≠45°时,①中的结论不发生变化.理由如下:
∵∠BAC=∠MBN=90°,AB=AC,BM=BN,
∴∠ABC=∠ACB=∠BNP=45°,
又∵∠BPN=∠APC,
∴△BNP∽△ACP,
∴![]() ,
,
又∵∠APB=∠CPN,
∴△ABP∽△CNP,
∴∠ANC=∠ABC=45°;
(2)∠ANC=90°﹣![]() ∠BAC.理由如下:
∠BAC.理由如下:
∵∠BAC=∠MBN≠90°,AB=AC,BM=BN,
∴∠ABC=∠ACB=∠BNP=![]() (180°﹣∠BAC),
(180°﹣∠BAC),
又∵∠BPN=∠APC,
∴△BNP∽△ACP,
∴![]() ,
,
又∵∠APB=∠CPN,
∴△ABP∽△CNP,
∴∠ANC=∠ABC,
在△ABC中,
∠ABC=![]() (180°﹣∠BAC)=90°﹣
(180°﹣∠BAC)=90°﹣![]() ∠BAC.
∠BAC.


科目:初中数学 来源: 题型:
【题目】李伟家客厅长6m,宽4.8m,计划在地面上铺方砖,要求地面上都是整块方砖,你会选择( )
A. 边长50cm的方砖B. 边长60cm的方砖C. 边长100cm的方砖D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+4x-6.
(1)将其化成y=a(x-h)2+k的形式;
(2)写出开口方向,对称轴方程,顶点坐标;
(3)求图象与两坐标轴的交点坐标;
(4)画出函数图象;
(5)说明其图象与抛物线y=x2的关系;
(6)当x取何值时,y随x增大而减小;
(7)当x取何值时,y>0,y=0,y<0;
(8)当x取何值时,函数y有最值?其最值是多少?
(9)当y取何值时,-4<x<0;
(10)求函数图象与两坐标轴交点所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一组数据a1 , a2 , …an的平均数和方差分别是5和3,那么一组新数据a1+2,a2+2,a3+2…,an+2平均数和方差是( )
A.5,3
B.5,4
C.7,3
D.7,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为估计鱼塘中鱼的数量,先从鱼塘中随机打捞50条鱼并在每条鱼上做上标记,然后等这50条鱼完全混合在鱼群中时再从鱼群中随机打捞50条,发现其中有2条鱼身上有前面做过的标记,则鱼塘中鱼的数量约有( )条.
A. 1200B. 1250C. 1300D. 1350
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(-1,0).设t=a+b+1,则t值的变化范围是( )

A. 0<t<1 B. 0<t<2 C. 1<t<2 D. -1<t<1
查看答案和解析>>
科目:初中数学 来源: 题型:
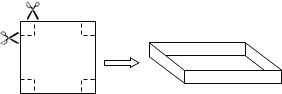
【题目】把一边长为40cm的正方形硬纸板,进行适当的剪裁,折成一个长方形盒子(纸板的厚度忽略不计).如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子.
(1)要使折成的长方形盒子的底面积为484cm2,那么剪掉的正方形的边长为多少?
(2)折成的长方形盒子的侧面积为600 cm2,那么剪掉的正方形的边长为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com