
��ͼ���ڡ�ABC�У���C=��ABC=2��A��BD��AC���ϵĸߣ����DBC�Ķ�����

 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ������
�������
��1��2x2��4x=12
��2��4x��2x+1��=6x+3��
(1)x=1����2��x=����x= �������������������1�����䷽�������� �������߳���2�Ѷ�����ϵ����Ϊ1��Ȼ��������һ����ϵ��һ���ƽ����ʹ���Ϊ��ȫƽ��ʽ���ұ��dz����Ȼ��ֱ�ӿ�ƽ����⼴�ɣ� ��2���ѷ����ұߵ����������ʽ3��������ߣ��������������ʽ(2x��1)��ʹ����ת��Ϊ������ʽ�Ļ�����0����ʽ��Ȼ��ת��Ϊ����һԪһ�η�����⼴�ɣ� ��������� ����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ���ѡ��
��ͼ����AB��OC������Ϊ��C������OA����OC��2��AB��4����OA���ڣ� ��

A. 2 B. 2
B. 2 C. 3
C. 3 D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ��4�� ����ƽ��ͼ�� ��Ԫ���Ծ� ���ͣ���ѡ��
��ͼ������OA��OB��ʾͬһ�����ߵ���(����)

A. ��A�� B. ��B�� C. ��C�� D. ��D��
B �����������������A�������෴����A����ͬһ�����ߣ� B���˵���ͬ��������ͬ����C��ͬһ�����ߣ� C������ͬ����D����ͬһ�����ߣ� D�������෴����B����ͬһ�����ߣ� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ������
��֪��MAN=120�㣬��C�ǡ�MAN��ƽ����AQ�ϵ�һ�����㣬��B��D�ֱ���AN��AM�ϣ�����BD��
�����֡�
��1����ͼ1������ABC=��ADC=90�㣬���BCD=�� ���㣬��CBD���� �������Σ�
��̽����
��2����ͼ2������ABC+��ADC=180�㣬���жϡ�CBD����״����֤����Ľ��ۣ�
��Ӧ�á�
��3����ͼ3����֪��EOF=120�㣬OPƽ�֡�EOF����OP=1������G��H�ֱ�������OE��OF�ϣ��ҡ�PGHΪ�ȱ������Σ����������������ġ�PGH�ĸ���һ������ ������ֻ����ţ�
��2�� ��3�� ��4�� ��4������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ������
��ͼ����ABC�ա� �����С�A=36��,��C=24�㣬���B=_____ .
�����С�A=36��,��C=24�㣬���B=_____ .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ڷ���ֽ�У���ABΪһ������ABP��ʹ֮���ABCȫ�ȣ��� �ĸ������ҳ����������ĵ�P�����P�У� ����.
�ĸ������ҳ����������ĵ�P�����P�У� ����.
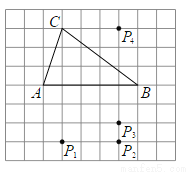
A. 1�� B. 2�� C. 3�� D. 4��
C �����������������Ҫʹ��ABP���ABCȫ�ȣ���P��AB�ľ���Ӧ�õ��ڵ�C��AB�ľ��룬��3����λ���ȣ��ʵ�P��λ�ÿ�����P1��P3��P4������ ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�гκ���2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
��һ�����κ�����ͼ����λͬѧ�ֱ�˵������һЩ�ص㣺
�ף���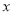 ��ֻ��һ�����㣻
��ֻ��һ�����㣻
�ң��Գ�����ֱ�� ��
��
������y��Ľ��㵽ԭ��ľ���Ϊ3��
��������ȫ���ص�Ķ��κ����Ľ���ʽΪ______________________��
�� ���������������: �߶��κ����ĶԳ���Ϊֱ��x=3�� ��k=3�� ����κ����Ľ���ʽΪ ����y��Ľ��㵽ԭ��ľ���Ϊ3�� ����y�ύ�ڵ�(0,3)��(0,?3)�� ��(0,3)����ã� ��(0,?3)����ã� �����ʽΪ�� ��. �ʴ�Ϊ�� ��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2017���^ѧ�ڽ�ѧ����������꼶��ѧ�Ծ� ���ͣ������
��֪��b�����ĸ���������a��b��c����|a+b|+��4��c��2016 =0���Իش����⣺
��1����ֱ��д��a��b��c��ֵ��
��2����a��b��c����Ӧ�ĵ�ֱ�ΪA��B��C����PΪһ���㣬���Ӧ����Ϊx����P��0��1֮���˶�ʱ����0��x��1�����뻯��ʽ�ӣ�|x+1|��|1-x|+2|x��4|��
��3���ڣ�1������2���������£���A��B��C��ʼ���������˶�������A��ÿ��2����λ���ȵ��ٶ������˶���ͬʱ����B��C�ֱ���ÿ��3����λ���Ⱥ�8����λ���ȵ��ٶ������˶�������t�������B���C֮��ľ����ʾΪBC����A��B֮��ľ����ʾΪAB�����ʣ�AB-BC��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
��1�� a=-1��b=1��c=4����2��8����3�� AB-BC��ֵ�Ƿ�����ʱ��t�ı仯���ı�. ����������������1������b�����ĸ����������ɵó�b��ֵ���ٸ��ݾ���ֵ��ż�η��ķǸ��Լ��ɵó�a��c��ֵ����2��������0��x��1ʱ��x+1��1-x��x-4��������ȥ������ֵ���ż��ɵó����ۣ���3���ҳ��˶�ʱ��Ϊtʱ����A��B��C��Ӧ�������ٸ��������ľ��빫ʽ�ҳ�AB��BC�ij��ȣ���������ɵ�...�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com