
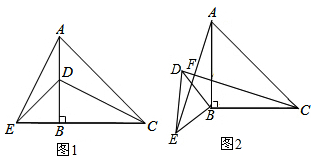
分析 (1)延长CD交AE于K,根据全等三角形的性质得到AE=CD,∠EAB=∠DCB,由于∠DCB+∠CDB=90°,于是得到结论;
(2)由于∠DBE=∠ABC=90°,得到∠ABE=∠DBC,根据全等三角形的性质得到AE=CD,∠EAB=∠DCB,等量代换得到∠KOA+∠KAO=90°,于是得到结论.
解答  解:(1)AE=CD,AE⊥CD,
解:(1)AE=CD,AE⊥CD,
理由:延长CD交AE于F,
在△AEB和△CDB中,
∵$\left\{\begin{array}{l}{∠ABE=∠CBD=90°}\\{AB=BC}\\{BE=DB}\end{array}\right.$,
∴△AEB≌△CDB(SAS)
∴AE=CD,
∠EAB=∠DCB,
∵∠DCB+∠CDB=90°,
∠ADF=∠CDB,
∴∠ADF+∠DAF=90°,
∴∠AFD=90°,
∴AE⊥CD;
(2)解:(2)AE=CD,AE⊥CD,
∵∠DBE=∠ABC=90°,
∴∠ABE=∠DBC,
在△AEB和△CDB中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠DBC}\\{BE=BD}\end{array}\right.$
∴△AEB≌△CDB,
∴AE=CD,∠EAB=∠DCB,
∵∠DCB+∠COB=90°,∠AOK=∠COB,
∴∠KOA+∠KAO=90°,
∴∠AKC=90°,
∴AE⊥CD.
点评 此题考查了全等三角形的判定与性质,用到的知识点全等三角形的判定与性质,关键是能在较复杂的图形中找出全等的三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数是15 | B. | 众数是10 | C. | 中位数是17 | D. | 方差是$\frac{44}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
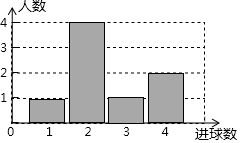 体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
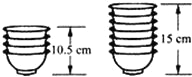 如图,两摞规格相同的碗整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题:
如图,两摞规格相同的碗整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com