
【题目】已知a、b、c是等腰三角形ABC的三条边的长,其中a=3,如果b、c是关于x的一元ニ次方程![]() -9
-9![]() +m=0的两个根,求m的値.
+m=0的两个根,求m的値.
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题的提出:
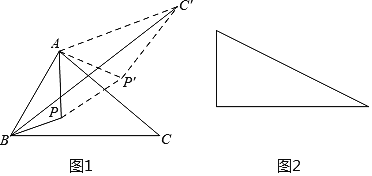
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到![]() 连接
连接![]() 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定![]() 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明:
![]() ;
;
问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
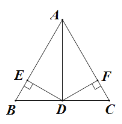
(1)求证:AB=AC;
(2)若∠BAC=60°,BC=6,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.
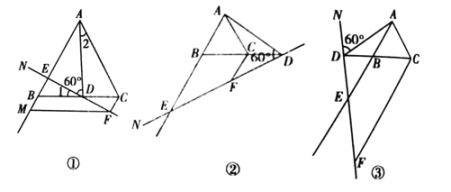
(1)当点D在线段BC上,∠NDB为锐角时,如图①.
①判断∠1与∠2的大小关系,并说明理由;
②过点F作FM∥BC交射线AB于点M,求证:CF+BE=CD;
(2)①当点D在线段BC的延长线上,∠NDB为锐角时,如图②,请直接写出线段CF,BE,CD之间的数量关系;
②当点D在线段CB的延长线上,∠NDB为钝角或直角时,如图③,请直接写出线段CF,BE,CD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
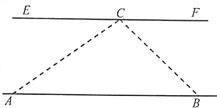
【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
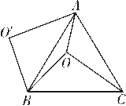
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;&
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AOBO′的面积为6+3![]() ;
;
⑤S△AOC+S△AOB=6+![]() .
.
其中正确的结论是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青年志愿者爱心小分队赴山村送温暖,准备为困难村民购买一些米面.已知购买1袋大米、4袋面粉,共需240元;购买2袋大米、1袋面粉,共需165元.
(1)求每袋大米和面粉各多少元?
(2)如果爱心小分队计划购买这些米面共40袋,总费用不超过2140元,那么至少购买多少袋面粉?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() ,
,
(1)求证:该一元二次方程总有两个实数根;
(2)若该方程只有一个小于4的根,求m的取值范围;
(3)若x1,x2为方程的两个根,且n=x12+x22﹣4,判断动点![]() 所形成的数图象是否经过点
所形成的数图象是否经过点![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com