
【题目】阅读理解
在⊙I中,弦AF与DE相交于点Q,则AQQF=DQQE.你可以利用这一性质解决问题.
问题解决
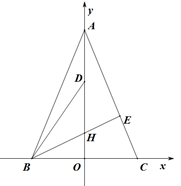
如图,在平面直角坐标系中,等边△ABC的边BC在x轴上,高AO在y轴的正半轴上,点Q(0,1)是等边△ABC的重心,过点Q的直线分别交边AB、AC于点D、E,直线DE绕点Q转动,设∠OQD=α(60°<α<120°),△ADE的外接圆⊙I交y轴正半轴于点F,连接EF.
(1)填空:AB= ;
(2)在直线DE绕点Q转动的过程中,猜想:![]() 与
与![]() 的值是否相等?试说明理由.
的值是否相等?试说明理由.
(3)①求证:AQ2=ADAE﹣DQQE;
②记AD=a,AE=b,DQ=m,QE=m(a、b、m、n均为正数),请直接写出mn的取值范围.

【答案】(1)2![]() (2)相等(3)①见详解;②
(2)相等(3)①见详解;②![]() ≤mn≤2.
≤mn≤2.
【解析】
(1)如图1,连接BQ,由点Q(0,1)是等边△ABC的重心,得到AQ=BQ=2OQ=2,∠QBO=30°,根据等边三角形的性质即可得到结论;
(2)根据等边三角形的性质得到∠DAF=∠FAE,根据相似三角形的性质得到![]() =
=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,等量代换即可得到结论;
,等量代换即可得到结论;
(3)①由相似三角形的性质得到![]() ,根据线段的和差得到ADAE=(AQ+QF)AQ,化简即可得到结论;②如图2,过点E作ET⊥AB于T,解直角三角形得到ET=AEsin60°=
,根据线段的和差得到ADAE=(AQ+QF)AQ,化简即可得到结论;②如图2,过点E作ET⊥AB于T,解直角三角形得到ET=AEsin60°=![]() b,求得S△ADE=
b,求得S△ADE=![]() ab,当α=90°时,此时DE∥x轴,S△ADE最小,根据相似三角形的性质得到
ab,当α=90°时,此时DE∥x轴,S△ADE最小,根据相似三角形的性质得到![]() ,得到
,得到![]() ,当α=120°时,此时DE经过点C,即点E和点C重合,S△ADE最大,根据三角形的面积得到
,当α=120°时,此时DE经过点C,即点E和点C重合,S△ADE最大,根据三角形的面积得到![]() ≤ab≤6,代入化简即可得到结论.
≤ab≤6,代入化简即可得到结论.
(1)如图1,连接BQ,∵点Q(0,1)是等边△ABC的重心,
∴AQ=BQ=2OQ=2,∠QBO=30°,∴AO=3,∴AB=sin60°AO=2![]() ;
;
故答案为:2![]() ;
;
(2)相等,
理由:∵AO为等边△ABC的高,∴AO平分∠BAC,∴∠DAF=∠FAE,又∠ADE=∠AFE,
∴△ADQ∽△AFE,∴![]() =
=![]() ,∵∠QEF=∠OAE,∠AFE=∠QFE,
,∵∠QEF=∠OAE,∠AFE=∠QFE,
∴△AFE∽△QEF,∴![]() ,∴
,∴![]() =
=![]() ;
;
(3)①∵△ADQ∽△AFE,∴![]() =
=![]() ,∴ADAE=AFAQ,即ADAE=(AQ+QF)AQ,
,∴ADAE=AFAQ,即ADAE=(AQ+QF)AQ,
∴ADAE=AQ2+AQQF,∵AQQF=DQQE,∴ADAE=AQ2+DQQE,即AQ2=ADAE﹣DQQE;
②如图2,过点E作ET⊥AB于T,在Rt△AET中,∠EAT=60°,ET=AEsin60°=![]() b,S△ADE=
b,S△ADE=![]() ADET=
ADET=![]() AD
AD![]() AE=
AE=![]() ADAE=
ADAE=![]() ab,当α=90°时,此时DE∥x轴,S△ADE最小,∴△ADE∽△ABC,∴
ab,当α=90°时,此时DE∥x轴,S△ADE最小,∴△ADE∽△ABC,∴![]() ,∴
,∴![]() ,又∵S△ABC=
,又∵S△ABC=![]() ×(2
×(2![]() )2=3
)2=3![]() ,∴
,∴![]() ,
,
当α=120°时,此时DE经过点C,即点E和点C重合,S△ADE最大,
∴S△ADE=![]() S△ABC=
S△ABC=![]() ×3
×3![]() =
=![]() ,∴
,∴![]() ≤ab≤
≤ab≤![]() ,
,
∴![]() ≤
≤![]() ab≤
ab≤![]() ,
,![]() ,由①证得:AQ/span>2=ADAE﹣DQQE,即22=ab﹣mn,
,由①证得:AQ/span>2=ADAE﹣DQQE,即22=ab﹣mn,
∴ab=mn+4,∴![]() ≤mn+4≤6,即
≤mn+4≤6,即![]() ≤mn≤2.
≤mn≤2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图1,荧光屏上的甲、乙两个光斑(可看作点)分别从相距8cm的A,B两点同时开始沿线段AB运动,运动工程中甲光斑与点A的距离S1(cm)与时间t(s)的函数关系图象如图2,乙光斑与点B的距离S2(cm)与时间t(s)的函数关系图象如图3,已知甲光斑全程的平均速度为1.5cm/s,且两图象中△P1O1Q1≌P2Q2O2,下列叙述正确的是( )

A. 甲光斑从点A到点B的运动速度是从点B到点A的运动速度的4倍
B. 乙光斑从点A到B的运动速度小于1.5cm/s
C. 甲乙两光斑全程的平均速度一样
D. 甲乙两光斑在运动过程中共相遇3次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB:y=![]() x+
x+![]() 分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
A. (0,4) B. (0,5) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为参加学校的“我爱古诗词”知识竞赛,王晓所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.请根据以上频率分布表和频率分布直方图,回答下列问题:
组别 | 分组 | 频数 | 频率 |
1 | 50≤x<60 | 9 | 0.18 |
2 | 60≤x<70 | a | b |
3 | 70≤x<80 | 21 | 0.42 |
4 | 80≤x<90 | m | 0.06 |
5 | 90≤x≤100 | 2 | n |
(1)求出a、b、m、n的值;
(2)老师说:“王晓的测试成绩是全班同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
(3)若要从小明、小敏等几位成绩优秀(分数在80≤x≤100范围内为优秀)的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:几位同学请用A、B、C、D…表示,其中小明为A,小敏为B)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
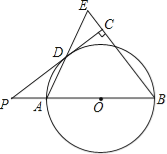
(1)求证:AB=BE;
(2)若PA=2,cosB=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为评估学生整理错题集的质量情况,进行了抽样调查,把学生整理错题集的质量分为“非常好”、“较好”、“一般”、“不好”四个等级,根据调查结果绘制了下面两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名学生;
(2)扇形统计图中,m= ,“非常好”部分所在扇形的圆心角度数为 ;
(3)补全条形统计图;
(4)如果4名学生整理错题集的质量情况是:3人“较好”,1人“一般”,现从中随机抽取2人,请用列表或画树状图的方法求出两人都是“较好”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=2x﹣4与x轴交于点A,与y轴交于点E,过点A作AE的垂线交y轴于点B,连接AB,以AB为边向上作正方形ABCD(如图所示),则点D的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产某种零件,每个零件的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,制定了促销条件:当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元.
(1)若销售商一次订购x(x>100)个零件,直接写出零件的实际出厂单价y(元)?
(2)设销售商一次订购x(x>100)个零件时,工厂获得的利润为W元(W>0).
①求出W(元)与x(个)之间的函数关系式及自变量x的取值范围;并算出销售商一次订购多少个零件时,厂家可获得利润6000元;
②厂家为了达到既鼓励销售商订购又保证自己能获取最大利润的目的,重新制定新促销条件:在原有的基础上又增加了限制条件﹣﹣销售商订购的全部零件的实际出厂单价不能低于a(元).请你利用函数及其图象的性质求出a的值;并写出实行新促销条件时W(元)与x(个)之间的函数关系式及自变量x的取值范围.(工厂出售一个零件利润=实际出厂单价﹣每个零件的成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com