
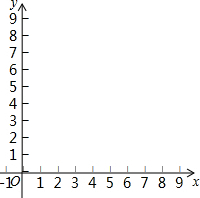 ��֪��һ�κ���y=-$\frac{3}{4}$x+6��ͼ����x�ύ��A����y�ύ��C����O��A��CΪ�����ڵ�һ����������OABC��
��֪��һ�κ���y=-$\frac{3}{4}$x+6��ͼ����x�ύ��A����y�ύ��C����O��A��CΪ�����ڵ�һ����������OABC������ ��1������y=-$\frac{3}{4}$x+6���A��C�����꣬���ɾ��ε����ʵó�B�����꣬��A��C��B�����꼴�ɻ�������y=-$\frac{3}{4}$x+6��ͼ��;���OABC��
��2����������ó�k��0�ҷ���$\frac{k}{x}=-\frac{3}{4}x+6$��ʵ���⣬�ó�����0��k��12�����ɵó�k��ȡֵ��Χ��
��3��������������ٵ�PB=PCʱ����P��BC�Ĵ�ֱƽ�����ϣ����ó���P�����ꣻ
�ڵ�PC=BCʱ��PC=BC=8�����ݹ��ɶ������AC���ó�AP����PD��OA��D����PD��OC���ó���ADP�ס�AOC���ó���Ӧ�߳ɱ������PD��AD�����OD�����ɵó���P�����꣮
��� �⣺��1����$y=-\frac{3}{4}x+6$=0����x=8��
��A��8��0����
��x=0ʱ��$y=-\frac{3}{4}x+6$=6��
��C��0��6����
���ı���ABCD�Ǿ��Σ�
���AOC=��OAB=��ABC=��OCB=90�㣬AB=OC=6��OA=BD=8��
��B��8��6����
����$y=-\frac{3}{4}x+6$��ͼ��;���OABC��ͼ1��ʾ��
��2������������$y=\frac{k}{x}$��x��0����ͼ�����OAC�й����㣬Ҳ�������߶�AC�й����㣬
��k��0�ҷ���$\frac{k}{x}=-\frac{3}{4}x+6$��ʵ���⣬
������-$\frac{3}{4}$x2+6x-k=0��ʵ���⣬
���=62-4����-$\frac{3}{4}$������-k����0��
��ã�k��12��
�֡�k��0��
��k��ȡֵ��Χ��0��k��12��
��3��������������ٵ�PB=PCʱ����P��BC�Ĵ�ֱƽ�����ϣ�
���P����������4��3����
�ڵ�PC=BCʱ��PC=BC=8��
��AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10��
��PA=AC-PC=2��
��PD��OA��D����ͼ2��ʾ�� ��PD��OC��
��PD��OC��
���ADP�ס�AOC��
��$\frac{PD}{OC}=\frac{AP}{AC}=\frac{AD}{OA}$��
��$\frac{PD}{6}=\frac{2}{10}=\frac{AD}{8}$��
��PD=$\frac{6}{5}$��AD=$\frac{8}{5}$��
��OD=8-$\frac{8}{5}$=$\frac{32}{5}$��
���P����������$\frac{32}{5}$��$\frac{6}{5}$����
������������P�������ǣ�4��3����$\frac{32}{5}��\frac{6}{5}$����
���� �����Ƿ����������ۺ���Ŀ��������������ͼ�����������ε����ʡ�һԪ���η��̵ĸ����б�ʽ�����ɶ��������������ε��ж������ʵ�֪ʶ�������ѶȽϴ��ۺ���ǿ���ر��ǣ�2����3���У���Ҫ����һԪ���η��̵ĸ����б�ʽ���������ۡ�֤�����������Ʋ��ܵó������


 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ����A=90�㣬AB=3��AD=4��CD=12��BC=13��
��֪����ͼ����A=90�㣬AB=3��AD=4��CD=12��BC=13���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У�AB=6��BC=8����E������CB�ϵ�һ�����㣬�ѡ�DCE��DE�۵�����C�Ķ�Ӧ��ΪC�䣮
��ͼ������ABCD�У�AB=6��BC=8����E������CB�ϵ�һ�����㣬�ѡ�DCE��DE�۵�����C�Ķ�Ӧ��ΪC�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����������ABCD�У���G��BC���ϵ�����һ�㣬DE��AG�ڵ�E��BF��DE����AG�ڵ�F����֤��AF=BF+EF��
��֪����������ABCD�У���G��BC���ϵ�����һ�㣬DE��AG�ڵ�E��BF��DE����AG�ڵ�F����֤��AF=BF+EF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
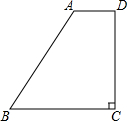 ��ͼ����һ�����οյ�ABCD�ɹ�ͣ����AD��BC����C=90�㣬��B=53�㣬AD=1.6m��CD=5.2m������һ����4.9m����1.9m��������Ҫ��ȫͣ�����������������һ��ͣ����������ͨ������˵�����ɣ����ο����ݣ�sin53���$\frac{4}{5}$��cos53���$\frac{3}{5}$��tan53���$\frac{4}{3}$��
��ͼ����һ�����οյ�ABCD�ɹ�ͣ����AD��BC����C=90�㣬��B=53�㣬AD=1.6m��CD=5.2m������һ����4.9m����1.9m��������Ҫ��ȫͣ�����������������һ��ͣ����������ͨ������˵�����ɣ����ο����ݣ�sin53���$\frac{4}{5}$��cos53���$\frac{3}{5}$��tan53���$\frac{4}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
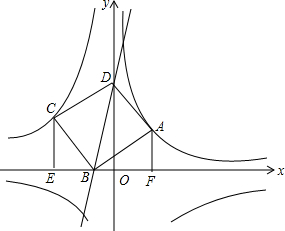 ��ͼ����A��2��2����˫����y1=$\frac{k}{x}$��x��0���ϣ���C��˫����y2=-$\frac{9}{x}$��x��0���ϣ��ֱ��A��C��x�������ߣ�����ֱ�ΪF��E����A��CΪ������������ABCD����ʹ��B��x���ϣ���D��y����������ϣ�
��ͼ����A��2��2����˫����y1=$\frac{k}{x}$��x��0���ϣ���C��˫����y2=-$\frac{9}{x}$��x��0���ϣ��ֱ��A��C��x�������ߣ�����ֱ�ΪF��E����A��CΪ������������ABCD����ʹ��B��x���ϣ���D��y����������ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
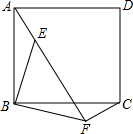 ��ͼ��EΪ������ABCD��һ�㣬��AEB��˳ʱ�뷽����תһ���ǶȺ��Ϊ��CFB������ת��90�ȣ�
��ͼ��EΪ������ABCD��һ�㣬��AEB��˳ʱ�뷽����תһ���ǶȺ��Ϊ��CFB������ת��90�ȣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com