
【题目】阅读下列材料:
在进行二次根式的化简与运算时,我们有时会碰上如![]() 样的式子,其实我们还可以将其进一步化简:
样的式子,其实我们还可以将其进一步化简:
(1)![]() ···(一)
···(一)
(2)![]() ···(二)
···(二)
(3) ···(三)
···(三)
以上这种化简的步骤叫做分母有理化.
![]() 还可以用以下方法化简:
还可以用以下方法化简: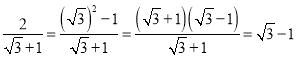 ···(四)
···(四)
请完成下列问题:
(1)请计算![]() ;
;
(2)当![]() ,则代数式
,则代数式![]() 的值为 ;
的值为 ;
(3)请参照(三)式和(四)式用两种不同的方法化简![]()
(4)化简:![]()
科目:初中数学 来源: 题型:
【题目】(1) [探索发现]正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() .求证:
.求证: ![]()
小玲想到的思路是:过点![]() 作
作![]() 于点
于点![]() 于点
于点![]() ,通过证明
,通过证明![]() 得到
得到![]() .请按小玲的思路写出证明过程
.请按小玲的思路写出证明过程

(2)[应用拓展]如图2,在![]() 的条件下,设正方形
的条件下,设正方形![]() 的边长为
的边长为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .求
.求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
【答案】A.
【解析】
试题分析:因为人和树均垂直于地面,所以和光线构成的两个直角三角形相似,
设树高x米,则![]() ,即
,即![]() ,解得,x=8. 故选A.
,解得,x=8. 故选A.
考点:相似三角形的应用.
【题型】单选题
【结束】
11
【题目】已知圆锥的底面半径为1cm,母线长为3cm,则其全面积为________cm2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 垂直
垂直![]() 轴于点
轴于点![]() ,且
,且![]() .
.
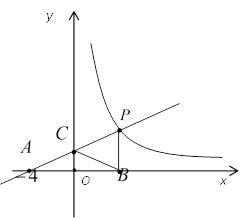
(1)仔细观察图形,直接写出![]() ;
;
(2)求![]() 和
和![]() 的值;
的值;
(3)在反比例函数图象上是否存在点![]() ,使四边形
,使四边形![]() 为平行四边形,如果存在,求出点
为平行四边形,如果存在,求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
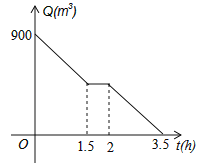
【题目】根据卫生防疫部门要求,游泳池必须定期换水,清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m2)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)暂停排水需要多少时间?排水孔排水速度是多少;
(2)当2≤t≤3.5时,求Q关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2.
(1)求∠A的正切值;
(2)若OC=1,求AB及![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款2.4万元,乙工程队工程款1万元.工程领导小组根据甲,乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用12天;
(3)若甲,乙两队合做6天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com