
����Ŀ��С�콫�ʼDZ�����ˮƽ�����������ϣ���ʾ��OB��װ�OA����ˮƽ�ߵļн�Ϊ120�㣬�о������ʣ���ͼ1��������ʾ��ͼΪͼ2��ʹ��ʱΪ��ɢ�ȣ����ڵװ��µ���ɢ�ȼ�ACO�����ת��AO��B��λ�ã���ͼ3��������ʾ��ͼΪͼ4����֪OA=OB=24cm��O��C��OA�ڵ�C��O��C=12cm�� 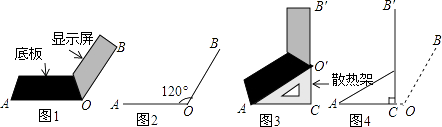
��1�����CAO��Ķ�����
��2����ʾ���Ķ���B���ԭ�������˶��٣�
��3����ͼ4������ɢ�ȼܺ�Ҫʹ��ʾ��O��B��ˮƽ�ߵļн��Ա���120�㣬����ʾ��O��B��Ӧ�Ƶ�O�䰴˳ʱ�뷽����ת���ٶȣ�
���𰸡�
��1���⣺��O��C��OA��C��OA=OB=24cm��
��sin��CAO��= ![]() ��
��
���CAO��=30��
��2���⣺����B��BD��AO��AO���ӳ�����D

��sin��BOD= ![]() ��
��
��BD=OBsin��BOD��
�ߡ�AOB=120�㣬
���BOD=60�㣬
��BD=OBsin��BOD=24�� ![]() =12
=12 ![]() ��
��
��O��C��OA����CAO��=30�㣬
���AO��C=60�㣬
�ߡ�AO��B��=120�㣬
���AO��B��+��AO��C=180�㣬
��O��B��+O��C��BD=24+12��12 ![]() =36��12
=36��12 ![]() ��
��
����ʾ���Ķ���B���ԭ�������ˣ�36��12 ![]() ��cm
��cm
��3���⣺��ʾ��O��B��Ӧ�Ƶ�O�䰴˳ʱ�뷽����ת30�㣬
���ɣ�����ʾ��O��B��ˮƽ�ߵļн��Ա���120�㣬
���EO��F=120�㣬
���FO��A=��CAO��=30�㣬
�ߡ�AO��B��=120�㣬
���EO��B��=��FO��A=30�㣬
����ʾ��O��B��Ӧ�Ƶ�O�䰴˳ʱ�뷽����ת30��
����������1��ͨ����ֱ�������μ��ɵõ��������2������B��BD��AO��AO���ӳ�����D��ͨ����ֱ�����������BD=OBsin��BOD=24�� ![]() =12
=12 ![]() ����C��O�䡢B�����㹲�߿ɵý������3����ʾ��O��B��Ӧ�Ƶ�O�䰴˳ʱ�뷽����ת30�㣬��á�EO��B��=��FO��A=30�㣬������ʾ��O��B��Ӧ�Ƶ�O�䰴˳ʱ�뷽����ת30�㣮
����C��O�䡢B�����㹲�߿ɵý������3����ʾ��O��B��Ӧ�Ƶ�O�䰴˳ʱ�뷽����ת30�㣬��á�EO��B��=��FO��A=30�㣬������ʾ��O��B��Ӧ�Ƶ�O�䰴˳ʱ�뷽����ת30�㣮
�����㾫����������Ŀ����֪������������ת�����ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���բ���ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��ˣ�


 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������C �ڡ�O �ϣ�����C ��ֱ����AB ���ӳ��߽��ڵ�P��AC=PC����COB=2��PCB��
��1����֤��PC �ǡ�O �����ߣ�
��2����֤�� ![]() ��
��
��3����M �ǻ�AB ���е㣬CM ��AB �ڵ�N����AB=8����MNMC ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ס����������Ÿ���Ա��400�ˣ�Ϊ�˽�����������Ա����������������������˳������飬�������£��벹�������� �ռ�����
�Ӽס����������Ÿ������ȡ20��Ա�����������������ܲ��ԣ����Գɼ����ٷ��ƣ����£�
�� 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
�� 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
��������������
�����·����������������������������ݣ�
�ɼ�x | 40��x��49 | 50��x��59 | 60��x��69 | 70��x��79 | 80��x��89 | 90��x��100 |
�� | 0 | 0 | 1 | 11 | 7 | 1 |
�� |
��˵�����ɼ�80�ּ�����Ϊ�����������㣬70����79��Ϊ�����������ã�60����69��Ϊ�������ܺϸ�60������Ϊ�������ܲ��ϸ�
��������
�����������ݵ�ƽ��������λ�����������±���ʾ��
���� | ƽ���� | ��λ�� | ���� |
�� | 78.3 | 77.5 | 75 |
�� | 78 | 80.5 | 81 |
�ó����ۣ�a�������Ҳ����������������Ա������Ϊ��b�������ƶϳ�����Ա������������ˮƽ�ϸߣ�����Ϊ �� �����ٴ�������ͬ�ĽǶ�˵���ƶϵĺ����ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵxOy�У���֪��A��0��1������P���߶�OA�ϣ���APΪ�뾶�ġ�P�ܳ�Ϊ1����M��A��ʼ�ء�P����ʱ�뷽��ת��������AM��x���ڵ�N��n��0�������Mת����·��Ϊm��0��m��1�������ŵ�M��ת������m�� ![]() �仯��
�仯�� ![]() ʱ����N��Ӧ�ƶ���·����Ϊ ��
ʱ����N��Ӧ�ƶ���·����Ϊ �� 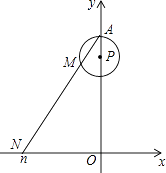
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���C=90�㣬BC=3��AC=4����P����CΪԲ�ģ�5Ϊ�뾶��Բ�ϣ�����PA��PB����PB=4����PA�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD��������AEFG�й�������A����������AEFG�Ƶ�A��˳ʱ�뷽����ת������ת�ǡ�DAG=��������0��ܦ���180�㣬����DF��BF����ͼ�� 
��1������=0�㣬��DF=BF�������֤����
��2���Ի�һ��ͼ�Σ�����������˵����1����������������Ǽ����⣻
��3�����ڣ�1��������������⣬����ܲ���һ����������ʹ��������Ϊ�����⣬��ֱ��д������Ϊ��Ҫ�����һ������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ��������������Ϣ���±���
ʱ��x���죩 | 1��x��50 | 50��x��90 |
�ۼۣ�Ԫ/���� | x+40 | 90 |
ÿ������������ | 200��2x | |
��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ��
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������y=��x2+bx+c����A��0����2����B����1��1�����㣬��ô�������߾����� ��
A.��һ����������������
B.��һ������������
C.��һ������������
D.�ڶ�������������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com