
【题目】如图1,Rt△ABC≌Rt△DFE,其中∠ACB=∠DFE=90°,BC=EF.
(1)若两个三角形按图2方式放置,AC、DF交于点O,连接AD、BO,则AF与CD的数量关系为 ,BO与AD的位置关系为 ;
(2)若两个三角形按图3方式放置,其中C、B(D)、F在一条直线上,连接AE,M为AE中点,连接FM、CM.探究线段FM与CM之间的关系,并证明;
(3)若两个三角形按图4方式放置,其中B、C(D)、F在一条直线上,点G、H分别为FC、AC的中点,连接GH、BE交于点K,求证:BK=EK.

【答案】(1)AF=CD, BO⊥AD;(2)FM=MC,FM⊥CM,理由见解析;(3)证明见解析.
【解析】
(1)利用全等三角形的性质,线段的垂直平分线的判定定理即可解决问题;
(2)结论:FM=MC,FM⊥CM.如图3中,延长FM交CA的延长线于H.想办法证明△FCH是等腰直角三角形,FM=MH即可解决问题;
(3)如图4中,连接BH,EG,在HG上取一点J,使得BJ=BH.想办法证明△BKJ≌△EKG即可解决问题;
(1)如图2中,
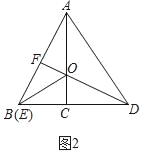
∵Rt△ABC≌Rt△DFE(已知),
∴AB=BD,BC=BF,
∴AF=CD,
∵∠AFO=∠DCO=90°,∠AOF=∠DOC,
∴△AOF≌△DOC(AAS),
∴OA=OC,∵BA=BD,
∴BO垂直平分线段AD.
∴BO⊥AD,
故答案为:AF=CD,BO⊥AD.
(2)结论:FM=MC,FM⊥CM.
理由:如图3中,延长FM交CA的延长线于H.
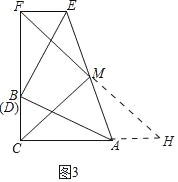
∵∠ACB+∠EFC=180°,B,F,C共线,
∴EF∥CH,
∴∠EFM=∠H,
∵EM=MA,∠EMF=∠AMH,
∴△EFM≌△AHM(AAS),
∴FM=MH,EF=AH,
∵∠FCH=90°,
∴CM=FM=MH,
即FM=MC,
∵△Rt△ABC≌Rt△DFE(已知),
∴BF=AC,EF=BC,
∴BA=AH,
∴FC=CH,
∵FM=MH,
∴CM⊥FM.
(3)如图4中,连接BH,EG,在HG上取一点J,使得BJ=BH.
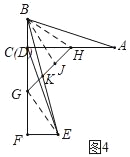
∵Rt△ABC≌Rt△DFE(已知),
∴BC=EF,AC=CF,
∵CH=AH,CG=GF,
∴CH=FG,
∵∠BCH=∠F=90°,
∴△BCH≌△EFG(SAS),
∴∠CBH=∠FEG,
∵CH=CG,∠GCH=90°,
∴∠CGH=∠CHG=45°,
∴∠BHG=180°﹣45°﹣∠GBH=135°﹣∠GBH,
∵∠CGE=∠CGH+∠HGE=90°+∠GEF,
∴∠HGE=45°+∠GEF,
∴∠HGE+∠BHG=180°,
∵∠BJK+∠BJH=180°,∠BJH=∠BHJ,
∴∠BJK=∠HGE,
∵GE=BH=BJ,∠BKJ=∠GKE,
∴△BKJ≌△EKG(AAS),
∴BJ=GE.


科目:初中数学 来源: 题型:
【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件:
(1)向上抛掷一枚均匀的硬币,出现正面朝上和反面朝上的可能性;
(2)掷一枚图钉,尖端朝地和尖端朝上的可能性;
(3)从一副扑克牌中任抽一张,抽到红桃和黑桃的可能性;
(4)有两个人用抓阄的方法定胜负,先抓获胜与后抓获胜的可能性.
其中可能性相等的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校课程安排中,各班每天下午只安排三节课.
(1)初一(1)班星期二下午安排了数学、英语、生物课各一节,通过画树状图求出把数学课安排在最后一节的概率;
(2)星期三下午,初二(1)班安排了数学、物理、政治课各一节,初二(2)班安排了数学、语文、地理课各一节,此时两班这六节课的每一种课表排法出现的概率是![]() .已知这两个班的数学课都由同一个老师担任,其他课由另外四位老师担任.求这两个班数学课不相冲突的概率.
.已知这两个班的数学课都由同一个老师担任,其他课由另外四位老师担任.求这两个班数学课不相冲突的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]()
(1) 如图1,若BD=DC,点C在AE的垂直平分线上。AB+BD与DE有什么关系?请给出证明。
(2) 如图2,若![]() , AB+BD与DE是否还存在(1)中的关系?若存在,请给出证明,若不存在,请说明理由。
, AB+BD与DE是否还存在(1)中的关系?若存在,请给出证明,若不存在,请说明理由。
(3) 若![]() ,则AB+AE与AD+BE有怎样的关系?答:AB+AE AD+BE (填“>”,“<”或“=”)
,则AB+AE与AD+BE有怎样的关系?答:AB+AE AD+BE (填“>”,“<”或“=”)

查看答案和解析>>
科目:初中数学 来源: 题型:
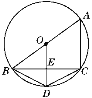
【题目】如图,四边形ABDC是⊙O的内接四边形,AB是⊙O的直径,OD⊥BC于E.
(1)请你写出四个不同类型的正确结论;
(2)若BE=4,AC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形网格中,若B(﹣3,﹣1),按要求回答下列问题:

(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出A和C的坐标;
(3)求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com