
【题目】如图,在⊙O中,AB是直径,AD是弦,∠ADE = 60°,∠C = 30°.
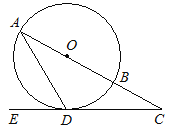
⑴判断直线CD是否是⊙O的切线,并说明理由;
⑵若CD = ![]() ,求BC的长.
,求BC的长.
【答案】(1)CD是⊙O的切线.
证明:如图,连接OD.
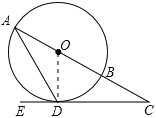
∵∠ADE=60°,∠C=30°,∴∠A=30°.
∵OA=OD,∴∠ODA=∠A=30°.
∴∠ODE=∠ODA+∠ADE=30°+60°=90°,∴OD⊥CD.
∴CD是⊙O的切线.
(2)解:在Rt△ODC中,∠ODC=90°, ∠C=30°, CD=![]() .
.
∵tanC=![]() ,
,
∴OD=CD·tanC=![]() ×
×![]() =3.
=3.
∴OC=2OD =6.
∵OB=OD=3,∴BC=OC-OB=6-3=3.
【解析】(1)根据切线的判定定理,连接OD,只需证明OD⊥CD,根据三角形的外角的性质得∠A=30°,再根据等边对等角得∠ADO=∠A,从而证明结论;
(2)在30°的直角三角形OCD中,求得OD,OC的长,则BC=OC-OB.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,公路![]() 为东西走向,在点
为东西走向,在点![]() 北偏东
北偏东![]() 方向上,距离
方向上,距离![]() 千米处是村庄
千米处是村庄![]() ,在点
,在点![]() 北偏东
北偏东![]() 方向上,距离
方向上,距离![]() 千米处是村庄
千米处是村庄![]() ;要在公路
;要在公路![]() 旁修建一个土特产收购站
旁修建一个土特产收购站![]() (取点
(取点![]() 在
在![]() 上),使得
上),使得![]() ,
,![]() 两村庄到
两村庄到![]() 站的距离之和最短,请在图中作出
站的距离之和最短,请在图中作出![]() 的位置(不写作法)并计算:
的位置(不写作法)并计算:
(1)![]() ,
,![]() 两村庄之间的距离;
两村庄之间的距离;
(2)![]() 到
到![]() 、
、![]() 距离之和的最小值.(参考数据:sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75计算结果保留根号.)
距离之和的最小值.(参考数据:sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75计算结果保留根号.)

查看答案和解析>>
科目:初中数学 来源: 题型:
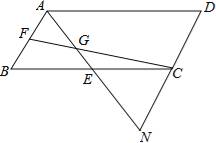
【题目】如图,在ABCD中,E,F分别为BC,AB中点,连接FC,AE,且AE与FC交于点G,AE的延长线与DC的延长线交于点N.
(1)求证:△ABE≌△NCE;
(2)若AB=3n,FB=![]() GE,试用含n的式子表示线段AN的长.
GE,试用含n的式子表示线段AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
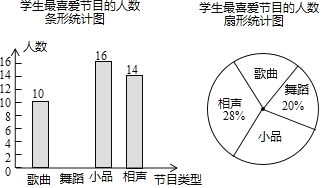
请你根据图中信息,回答下列问题:
(1)本次共调查了 名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于 度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为 人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①② B. ①③ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠A=60°,AB=6厘米,BC=12厘米,点P、Q同时从 顶点A出发,点P沿A→B→C→D方向以2厘米/秒的速度前进,点Q沿A→D方向以1厘米/秒的速度前进,当Q到达点D时,两个点随之停止运动.设运动时间为x秒,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x的函数图象大致是( )
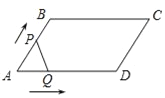
A. 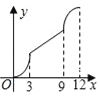 B.
B. 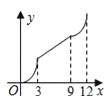 C.
C. 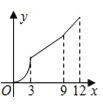 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(-2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
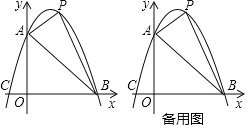
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com