
 数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为30°,已知BE=2m,此学生身高CD=1.7m,求大树的高度.(结果保留根号)
数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为30°,已知BE=2m,此学生身高CD=1.7m,求大树的高度.(结果保留根号) 分析 根据题意结合坡度的定义得出C到AB的距离,进而利用锐角三角函数关系得出AB的长.
解答 解:如图所示:过点C作CG⊥AB延长线于点G,交EF于点N,
由题意可得:$\frac{EF}{DF}$=$\frac{1}{4}$=$\frac{EF}{8}$,
解得:EF=2,
∵DC=1.7m,
∴FN=1.7m,
∴BG=EN=0.3m,
∵GN=EB=2m,
∴CG=CN+NG=10m,
在Rt△ACG中,tan30°=$\frac{AG}{CG}$,
∴AG=CG•$\frac{\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}$
则AB=AG-BG=$\frac{10\sqrt{3}}{3}$-$\frac{3}{10}$=$\frac{100\sqrt{3}-9}{30}$(m),
答:大树高度AB为$\frac{100\sqrt{3}-9}{30}$m.
点评 此题主要考查了解直角三角形的应用以及坡度的定义,正确得出C到AB的距离是解题关键.


科目:初中数学 来源: 题型:选择题
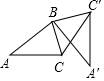 如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )
如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )| A. | 2$\sqrt{2}$ | B. | -2 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
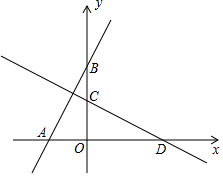 如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.
如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com