
【题目】已知A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A. 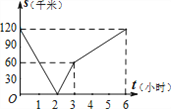 B.
B. 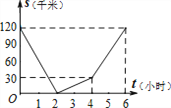
C.  D.
D. 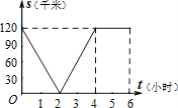
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】反比例函数![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数![]() 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.
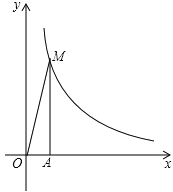
(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数![]() 的图象上,求t的值.
的图象上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=6,AC=8,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为(
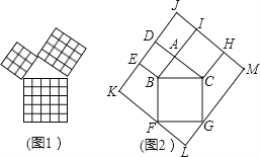
A. 360 B. 400 C. 440 D. 484
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求下列各式中的x的值:
(1)8x3+125=0;
(2)(x-3)2-9=0.
【答案】(1)x=-![]() ;(2)x1=6或x2=0.
;(2)x1=6或x2=0.
【解析】试题分析:(1)立方根定义解方程.(2)平方根定义解方程.
试题解析:(1)8x3+125=0,
x3=![]() ,
,
x=-![]() .
.
(2)(x-3)2-9=0,
(x-3)2=9,
x-3=![]() ,
,
x1=6或x2=0.
【题型】解答题
【结束】
19
【题目】(1)已知某数的平方根是![]() 和
和![]() ,
, ![]() 的立方根是
的立方根是![]() ,求
,求![]() 的平方根.
的平方根.
(2)已知y=![]() +
+![]() -8,求
-8,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2
(1)是一元二次方程;
(2)是一元一次方程;
(3)若x=﹣2是它的一个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:①GA=GP;②∠DCP=45°;③BP垂直平分CE;④GF+ FC =GA;其中正确的判断有______________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:

解:因为AD∥BC(已知),
所以∠1=∠3( ).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥________( ).
所以∠3+∠4=180°( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com