
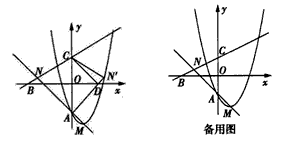
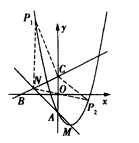
已知:抛物线y=x2-2x+a(a<0)与y 轴相交于点A,顶点为M,直线 分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N。
分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N。
(1)填空:试用含a的代数式分别表示点M与N的坐标,则M( ,),N(____,____);
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a 的值和四边形ADCN的面积;
(3)在抛物线y=x2-2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形? 若存在,求出P点的坐标;若不存在,试说明理由。
解:(1)M(1,a-1),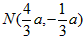 ; ; |
|
| (2)由题意得点N与点N′关于y轴对称, ∴ 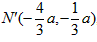 将N′的坐标代入y=x2-2x+a, 得 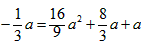 ∴a1=0(不合题意,舍去), 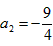 ∴ 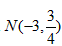 ∴点N到y轴的距离为3, ∴ 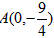 , ,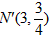 ∴直线AN′的解析式为  , ,它与x轴的交点为 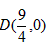 , ,∴点D到y轴的距离为 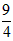 , ,∵直线BC与y轴的交点为 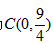 , ,∴S四边形ADCN =S△ACN +S△ACD= 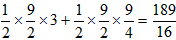 ; ; |
|
| (3)①当点P在y轴的左侧时,若四边形ACPN是平行四边形,则PN平行且等于AC,如图所示, ∴把N向上平移-2a个单位得到点P,P点坐标为 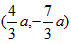 ,把点P的坐标代人抛物线的解析式, ,把点P的坐标代人抛物线的解析式,得: 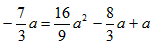 ∴a1=0(不合题意,舍去), 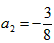 ∴ 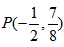 ; ;②当点P在y轴的右侧时,若四边形APCN是平行四边形,则AC与PN互相平分,如图所示, ∴OA=OC,OP=ON, ∴P与N关于原点对称 ∴ 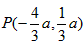 ∴将P点坐标代入抛物线解析式得:  ∴a1=0(不合题意,舍去), 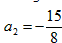 ∴ 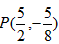 综上所述,存在这样的点 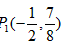 或 或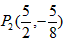 使得以P、A、C、N为顶点的四边形是平行四边形。 使得以P、A、C、N为顶点的四边形是平行四边形。 |
 |


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com