
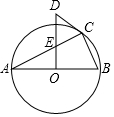
 如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.分析 (1)由圆周角定理得出∠ACB=90°,由勾股定理求出AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{5}$,得出OA=$\frac{1}{2}$AB=$\sqrt{5}$,证明△AOE∽△ACB,得出对应边成比例即可得出答案;(2)连接OC,由等腰三角形的性质得出∠1=∠A,由切线的性质得出OC⊥CD,得出∠2+∠CDE=90°,证出∠3=∠CDE,再由三角形的外角性质即可得出结论.
解答 解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴OA=$\frac{1}{2}$AB=$\sqrt{5}$,
∵OD⊥AB,
∴∠AOE=∠ACB=90°,
又∵∠A=∠A,
∴△AOE∽△ACB,
∴$\frac{OE}{BC}=\frac{OA}{AC}$,即$\frac{OE}{2}=\frac{\sqrt{5}}{4}$,
解得:OE=$\frac{\sqrt{5}}{2}$;
(2)∠CDE=2∠A,理由如下:
连接OC,如图所示:
∵OA=OC,
∴∠1=∠A,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠2+∠CDE=90°,
∵OD⊥AB,
∴∠2+∠3=90°,
∴∠3=∠CDE,
∵∠3=∠A+∠1=2∠A,
∴∠CDE=2∠A.
点评 本题考查了切线的性质、圆周角定理、勾股定理、相似三角形的判定与性质、等腰三角形的性质、直角三角形的性质、三角形的外角性质;熟练掌握圆周角定理和切线的性质是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
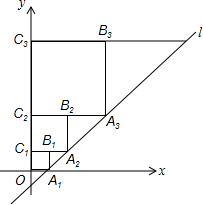 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031.
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).
为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
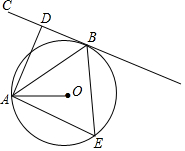 如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\sqrt{2}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{1}{5}}$ | D. | $\sqrt{a^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com