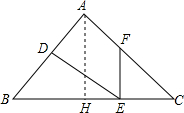
△ABC中,AB=AC=10,BC=12,动点D在边AB上,DE⊥AB,点E在BC上,点F在边AC上,且∠DEF=∠B,当点D在AB上运动时,
(1)S△FCE可能等于S△EBD的二倍吗?若可能,请求出BD的长;若不可能,请说明理由.
(2)S△FCE可能等于S△EBD的四倍吗?若可能,请求出BD的长;若不可能,请说明理由.
(1)存在.
证明:如图所示:
过点A作AH⊥BC于点H,
∵DE⊥AB,
∴∠B+∠BED=90°,
∵∠DEF=∠B,
∴∠BED+∠DEF=90°,
∴FE⊥BC,
∴∠BDE=∠CEF,
∵AB=AC,
∴∠B=∠C,
∴△EBD∽△FCE,
∵BC=12,AB=AC,AH⊥BC,
∴BH=CH=6,AH=8,
∵FE⊥BC,
∴当点F与点A重合时△FCE的面积最大,此时点E与点H重合,
∴S
△FCE=

CE•EF=

×6×8=24;
∵
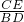
=

=
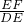
,
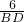
=

=
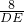
,解得BD=3.6,DE=4.8,
∴S
△EBD=

BD•DE=

×3.6×4.8=8.64,
∵2×8.64=9.2<24,
∴S
△FCE可能等于S
△EBD的2倍;
(2)不存在.
证明:由(1)知当点F与点A重合时△FCE的面积最大,此时点E与点H重合,S
△FCE=

CE•EF=

×6×8=24,S
△EBD=

BD•DE=

×3.6×4.8=8.64,
∵24<4×8.64=34.56,点F只在AC边上,
∴S
△FCE不可能等于S
△EBD的四倍.
分析:(1)根据题意画出图形,过点A作AH⊥BC于点H,根据相似三角形的判定定理得出△EBD∽△FCE,当点F到达A点时△FCE的面积最大,求出两三角形面积的值进行比较即可;
(2)根据(1)中两三角形的面积即可得出结论.
点评:本题考查的是相似三角形的判定与性质,根据题意画出图形利用数形结合是解答此题的关键.

 (1)存在.
(1)存在. CE•EF=
CE•EF= ×6×8=24;
×6×8=24;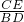 =
= =
=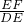 ,
,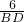 =
= =
=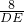 ,解得BD=3.6,DE=4.8,
,解得BD=3.6,DE=4.8, BD•DE=
BD•DE= ×3.6×4.8=8.64,
×3.6×4.8=8.64, CE•EF=
CE•EF= ×6×8=24,S△EBD=
×6×8=24,S△EBD= BD•DE=
BD•DE= ×3.6×4.8=8.64,
×3.6×4.8=8.64,

 名校课堂系列答案
名校课堂系列答案 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°, ,连接AO、BE、DC.
,连接AO、BE、DC.