
 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).分析 (1)当点Q与点C重合时,由等腰直角三角形的性质得出AP=BP=$\frac{1}{2}$AB=4$\sqrt{2}$,求出4$\sqrt{2}$÷$\sqrt{2}$=4(s)即可;
(2)分三种情形①当0<t≤4时,设PR、PQ分别交AB于点E、F,则重叠部分为△PEF,②当4<t≤$\frac{16}{3}$时,如图3中,设PR、RQ分别交AD于E、G,则重叠部分为四边形PEGQ.③当$\frac{16}{3}$<t<8时,如图4中,则重合部分为△PRQ,分别计算即可解决问题.
(3)分情况讨论:①根据三角形的面积关系得:AM=BM=$\frac{1}{2}$AB=4$\sqrt{2}$,根据等腰直角三角形的性质得:PM=PB=$\frac{1}{2}$BM,得出AP=$\frac{3}{4}$AB=6$\sqrt{2}$,即可得出结果;
②如图⑤所示:同②得:t=$\frac{32}{5}$;③如图⑥所示:设BR交AC于M,AP=$\sqrt{2}$t,根据三角形的面积关系得:AM=CM=$\frac{1}{2}$AC=4,根据等腰直角三角形的性质得:AM=$\sqrt{2}$AP=2t,得出2t=4,解得t=2;即可得出答案.
解答 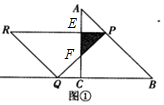 解:(1)当点Q与点C重合时,
解:(1)当点Q与点C重合时,
∵PQ⊥AB,△ABC是等腰直角三角形,
∴AP=BP=$\frac{1}{2}$AB=4$\sqrt{2}$,
∴4$\sqrt{2}$÷$\sqrt{2}$=4(s),
即当点Q与点C重合时,t=4;
故答案为:4;
(2)①当0<t≤4时,
如图①中,设PR、PQ分别交AB于点E、F,则重叠部分为△PEF,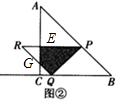
∵AP=$\sqrt{2}$t,
∴EF=PE=t,
∴S=S△PEF=$\frac{1}{2}$•PE•EF=$\frac{1}{2}$t2.
②当4<t≤$\frac{16}{3}$时,如图②中,设PR、RQ分别交AB于E、G,
则重叠部分为四边形PEGQ.
∵PQ=PC=8$\sqrt{2}$-$\sqrt{2}$t,
∴PR=16-2t,
∴RE=PR-PE=16-3t,
∴S=S△PRQ-S△REG=$\frac{1}{2}$(8$\sqrt{2}$-$\sqrt{2}$t)2-$\frac{1}{2}$(16-3t)2=-$\frac{7}{2}$t2+32t-64.
③当$\frac{16}{3}$<t<8时,如图③中,则重合部分为△PRQ,
∴S=S△PRQ=$\frac{1}{2}$PQ2=$\frac{1}{2}$(8$\sqrt{2}$-$\sqrt{2}$t)2=t2-16t+64.
(3)分情况讨论: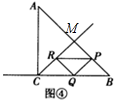
①如图④所示:
根据三角形的面积关系得:AM=BM=$\frac{1}{2}$AB=4$\sqrt{2}$,
根据等腰直角三角形的性质得:PM=PB=$\frac{1}{2}$BM,
∴AP=$\frac{3}{4}$AB=6$\sqrt{2}$,
∴$\sqrt{2}$t=6$\sqrt{2}$,
解得:t=6;
②如图⑤所示:同②得:t=$\frac{32}{5}$;
③如图⑥所示:
设BR交AC于M,AP=$\sqrt{2}$t,
根据三角形的面积关系得:AM=CM=$\frac{1}{2}$AC=4,
根据等腰直角三角形的性质得:AM=$\sqrt{2}$AP=2t,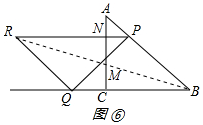
∴2t=4,
∴t=2;
综上所述:点R与△ABC的顶点的连线平分△ABC面积时t的值为6或$\frac{32}{5}$或2.
点评 本题是三角形综合题;考查了等腰直角三角形的性质、分段函数、三角形面积等知识,解题的关键是正确画出图象,学会分类讨论,属于中考压轴题.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,…则顶点M2017的坐标为(4033,4033).
如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,…则顶点M2017的坐标为(4033,4033).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
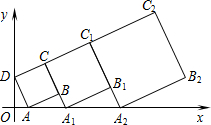 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是( )| A. | 10×($\frac{4}{3}$)4030 | B. | 10×($\frac{4}{3}$)4031 | C. | 10×($\frac{4}{3}$)4032 | D. | 10×($\frac{4}{3}$)4033 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每户每月用水量 | 水费价格(单位:元/吨) |
| 不超过20 | 2.3 |
| 超过20吨且不超过30吨的部分 | a |
| 超过30吨的部分 | 4.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
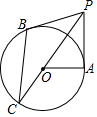 如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.
如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示,则乙比甲每小时快( )
甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示,则乙比甲每小时快( )| A. | 20km/h | B. | 30km/h | C. | 40km/h | D. | 50km/h |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com