
����Ŀ����ʦ�������˱�ѧ��ѧ�����������������������Ƴ�����ͼ��ͼ1���Ͳ�����������ͼ��ͼ2������������ͼ��ī���ڸ���һ���֣�
��1��������ͼ�б��ڸǵ�������д����������λ����
��2����������ѧ�������ѡһ��̸������룬��ѡ�ж��鳬��5���ѧ���ĸ��ʣ�
��3������ֲ��������⼸�ˣ���֪���ٵĶ���6�ᣬ������֮ǰ�����ݺϲ����ֲ�������λ��û�ı䣬����ಹ������ ���ˣ�

���𰸡���1������ͼ�б��ڸǵ���Ϊ9����������λ��Ϊ5����2��ѡ�ж��鳬��5���ѧ���ĸ���Ϊ![]() ����3��3
����3��3
����������1���ö���Ϊ6���������������ռ�İٷֱȵõ�������������������������ֱ��ȥ����Ϊ4�ᡢ6���7��������õ�����5���������Ȼ�������λ���Ķ������������λ����
��2���ö���Ϊ6���7��������ͳ����������õ�ѡ�ж��鳬��5���ѧ���ĸ��ʣ�
��3��������λ���Ķ�����ж����������ܳ���27���Ӷ��õ���ಹ���������
��1������ѧ������Ϊ6��25%=24���ˣ���
����Ϊ5���ѧ����Ϊ24��5��6��4=9���ˣ���
��������ͼ�б��ڸǵ���Ϊ9����������λ��Ϊ5��
��2��ѡ�ж��鳬��5���ѧ���ĸ���=![]() ��
��
��3����Ϊ4���5���������Ϊ14����λ��û�ı䣬�������������ܳ���27������ಹ����3�ˣ�
�ʴ�Ϊ��3��


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
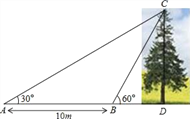
����Ŀ����ͼ��ij��ѧ��ȤС�������һ����CD�ĸ߶ȣ��������ڵ�A���������C������Ϊ30�㣬Ȼ����AD����ǰ��10m������B�㣬��B���������C�����Ǹ߶�Ϊ60�㣨A��B��D������ͬһֱ���ϣ�������������Dz������ݼ��������CD�ĸ߶ȣ������ȷ��0.1m�������ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
���𰸡�8.7��
������������������������������ε���ǵ����������ACB�Ķ������õ�BC�ij��ȣ�Ȼ����ֱ����BDC�У��������Ǻ���������⣮
����������ߡ�CBD=��A+��ACB��
���ACB=��CBD����A=60�㩁30��=30����
���A=��ACB��
��BC=AB=10���ף���
��ֱ����BCD�У�CD=BCsin��CBD=10��![]() =5
=5![]() ��5��1.732=8.7���ף���
��5��1.732=8.7���ף���
�������CD�ĸ߶�Ϊ8.7�ף�
���㣺��ֱ�������ε�Ӧ��
�����͡������
��������
23
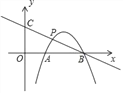
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=��x2+ax+b��x����A��1��0����B��3��0�����㣬��P�����������ڵ�һ�����ڵ�һ�㣬ֱ��BP��y���ཻ�ڵ�C��
��1����������y=��x2+ax+b�Ľ���ʽ��
��2������P���߶�BC���е�ʱ�����P�����ꣻ
��3���ڣ�2���������£���sin��OCB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��|a|+|b|��|a+b|����a��b��ϵ�ǣ�������
A. a��b�ľ���ֵ���
B. a��b���
C. a+b�ĺ��ǷǸ���
D. a��bͬ�Ż�a��b����һ��Ϊ0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У�����A+��B����C������A����B����C��1��5��6������A��90�㩁��B������A����B��![]() ��C�У���ȷ����ABC��ֱ�������ε������У�������
��C�У���ȷ����ABC��ֱ�������ε������У�������
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ӭ��ȫ���������д������н����ӵ�һ��������һ����������Ĺ�·��Ѳ�ߣ�����涨��Ϊ��������Ϊ�����ӳ����㿪ʼ���ߵ�·��Ϊ��+2��-3��+2��+1��-2��-1��-2����λ��ǧ�ף�
��1���������������˾�������ӳ���������λ�ã�
��2�������ʱ��������㶫��2ǧ�״����ֽ�ͨ�¹ʣ��ӳ����������ϸ����ֳ����ã����ڴ˴�Ѳ�ߺʹ����¹��й����Ͷ�����������֪ÿǧ����0.2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Գdz���һ��̨ʽ���Ժ�Һ����ʾ��������ÿ̨����2000Ԫ��Һ����ʾ��ÿ������400Ԫ.�����ڼ俪չ���������ͻ��ṩ�����Żݷ�����
�����٣���һ̨������һ��Һ����ʾ����
�����ڣ����Ժ�Һ����ʾ���������۵�![]() ����.
����.
��ѧУҪ�����������豸�����õ��Գǹ������30̨��Һ����ʾ��![]() ����
����![]() ����
����
��1����ѧУ�ֱ𰴷����ٻ��ڹ����踶�����Ԫ�����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2����![]() ��ͨ������˵����ʱѧУ�����ַ��������Ϊ���㣿
��ͨ������˵����ʱѧУ�����ַ��������Ϊ���㣿
��3����![]() ʱ������ΪѧУ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ���.
ʱ������ΪѧУ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��D��B��E�ĵ���ͬһ��ֱ���ϣ�AD��BE��BC��EF��BC��EF��

��1����֤��AC��DF��
��2����CDΪ��ACB��ƽ���ߣ���A��25������E��71�������CDF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ�������ABC�߳��Ƕ�ֵ����O���������ģ�����O������һ��ֱ�߷ֱ�AB��BC�ڵ�D��E������BDE��ֱ��DE�۵����õ���B��DE����B��D��B��E�ֱ�AC�ڵ�F��G������OF��OG���������жϴ�����ǣ�������
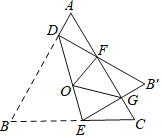
A. ��ADF�ա�CGE
B. ��B��FG���ܳ���һ����ֵ
C. �ı���FOEC�������һ����ֵ
D. �ı���OGB'F�������һ����ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCΪ�ȱ������Σ���ƽ������һ��P��ʹ��PAB����PBC����PAC��Ϊ���������Σ��������ĵ�P�ĸ���Ϊ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com