
 如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2$\sqrt{3}$,且AB、AE的长是关于x的方程x2-8x+k=0的两个实数根.
如图,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.若AD=2$\sqrt{3}$,且AB、AE的长是关于x的方程x2-8x+k=0的两个实数根.分析 (1)根据切线长定理得出AB•AE的长=12,进而得出k的值,设半径的长为r,再代入切线长定理解答即可;
(2)根据切线长定理,即可得出CD=CB,由勾股定理得CD的长即可.
解答 解:(1)连接OD、DE、DB,设⊙O半径为r,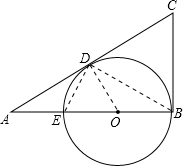
∵CD为⊙O切线,∴∠ODA=90°,
∵BE为⊙O直径,∴∠BDE=90°,
∴∠ADE=∠BDO,
∵OB=OD,∴∠OBD=∠ODB,
∵∠DAE=∠BAD,
∴△ADE∽△ABD,
∴$\frac{AD}{AB}=\frac{AE}{AD}$,
∴AB•AE=$A{D}^{2}=(2\sqrt{3})^{2}=12$,
∵AB、AE的长是关于x的方程x2-8x+k=0的两个实数根,
∴k=12,
解方程x2-8x+12=0得:两个实数根为:2和6,
∴设半径的长为r,
可得半径r=$\frac{1}{2}$×(6-2)=2;
(2)∵∠B=90°,
∴CB为⊙O切线,
∴CD=CB,
∴CB2+AB2=AC2,
∴CD2+62=(2$\sqrt{3}$+CD)2,
∴CD=2$\sqrt{3}$.
答:CD的长度为2$\sqrt{3}$.
点评 本题考查了切线的性质,以及相似三角形、勾股定理和切线长定理,要注意知识点之间的综合运用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.
如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3•a2=a6 | B. | (-a3)2=a6 | C. | 2a+3a2=5a3 | D. | $3{a^3}÷2a=\frac{3}{2}{a^3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 把一个圆球放置在V形架中,如图是它的平面示意图,CA和CB都是圆O的切线,切点分别是A、B,测得∠ACB=60°,且C点到切点B的距离为6cm,则圆球的半径是2$\sqrt{3}$.
把一个圆球放置在V形架中,如图是它的平面示意图,CA和CB都是圆O的切线,切点分别是A、B,测得∠ACB=60°,且C点到切点B的距离为6cm,则圆球的半径是2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.
如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
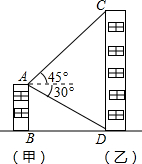 如图,甲楼AB的高度为21m,在甲楼楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°.求乙楼CD的高度(结果精确到0.1米,$\sqrt{3}$≈1.73,$\sqrt{2}$,1.41)
如图,甲楼AB的高度为21m,在甲楼楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°.求乙楼CD的高度(结果精确到0.1米,$\sqrt{3}$≈1.73,$\sqrt{2}$,1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
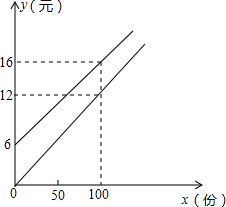 我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com