
分析 这是关于数学的应用性看法的数学短文,注意联系相关知识及现实生活,学以致用.
解答 解:有趣的勾股数
在学习和运用勾股定理时,如果深入了解一下勾股数的一些特征,不仅能十分方便地熟记勾股弦的相关数值并运用到三角和几何里,而且使我们对勾股数的认识和掌握更加方便、易记.
我们知道,在一个直角三角形中,斜边为弦,两直角边中短者为勾,长者为股.它们满足勾2+股2=弦2,当勾,股,弦都是整数时,比如当勾=5,股=12,弦=13时,我们称之为一组“勾股数”或“毕达哥拉斯数”.大家常说的“勾三股四弦五”就是一组勾股数.我们可以举出无穷多组的勾股数来,如:
62+82=102 72+242=252 82+152=172
92+402=412 172+1442=1452 202+212=292….、
大家是否想到这些勾股数尚有不少有趣的特征呢.
特征1:任意一组勾股数中,必有一个数是3的倍数;必有一个数是4的倍数;必有一个数是5的倍数.
如:6,8,10是一组勾股数,其中6是3的倍数,8是4的倍数,10是5的倍数.又如9,40,41是一组勾股数,其中9是3的倍数,40既是4的倍数也是5的倍数.
特征2:在所有的勾股数中,其中没有一组的三个数都是奇数的.
下面我们采用“反证法”来证明.
假设一组勾股数都是奇数为:2X1+1,2X2+1,2X3+1(X1,X2,X3 皆为整数)
它们分别平方后得到:(2X1+1)2=4 X12 +4 X1 +1,(2X2+1)2=4 X22 +4 X2 +1,
(2X3+1)2=4 X32 +4 X3 +1
把这三个数中的任意两个加起来,如:(2X1+1)2+(2X2+1)2=2(2X12 +2X22 +2X1 +2 X2+1)其和是一个偶数,而(2X3+1)2 却是一个奇数,二者显然不等.
由此可见三个都是奇数的勾股数是不存在的.
特征3:若a,b,c是一组勾股数,则ka,kb,kc(k是任意自然数)也是一组勾股数.
这个特征的证明则更简单:由a2+b2=c2,有(ka)2+(kb)2=k2(a2+b2)=(kc)2.
从而得出(ka)2+(kb)2=(kc)2.
这个特征告诉我们,只要知道一组勾股数,便可得到无数多组的勾股数.尽管如此,我们却只能得到部分勾股数,其余的勾股数是否能用简单的代数公式给出呢?为此,我们再将一些勾股数进行归类考察:
3,4,5 7,24,25 5,12,13 9,40,41
6,8,10 10,24,26 8,15,17 12,35,37
从中可以发现这些勾股数的组成规律,
特征4:象第一组,如果第一个数是奇数,那么第二个数是第一个数的平方减1再除以2,第三个数是第二个数加1.写成公式:若M为奇数,则M,$\frac{{M}^{2}-1}{2}$,$\frac{{M}^{2}+1}{2}$,就是一组勾股数.
同样,我们可以写成第二组的勾股数公式:
N,($\frac{N}{2}$)2-1,($\frac{N}{2}$)2+1,(N是偶数)
了解勾股数的这些有趣特征,就对勾股数有了较深刻的认识,也就掌握了它们的组成规律.在学习数学、物理时灵活运用这些有趣的特征,可收事半功倍之效.
点评 考查了应用类问题,本题是开放型写作题目,比较新颖,答案不唯一,同学们可以自由发挥.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
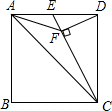 如图,在正方形ABCD中,E是AD的中点,DF⊥EC于点F,连结AF,则下列四个结论:
如图,在正方形ABCD中,E是AD的中点,DF⊥EC于点F,连结AF,则下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com