
分析 (1)先化简题目中的式子,然后合并同类项即可解答本题;
(2)根据平方差公式可以解答本题;
(3)根据多项式乘多项式可以多项式除以单项式可以解答本题;
(4)根据完全平方公式、平方差公式可以解答本题.
解答 解:(1)$\sqrt{\frac{1}{4}}$-$\root{3}{-8}$+2×$\sqrt{(-2)^{2}}$
=$\frac{1}{2}-(-2)+2×2$
=$\frac{1}{2}+2+4$
=6.5;
(2)$\frac{201{4}^{2}}{2013×2015+1}$
=$\frac{201{4}^{2}}{(2014-1)(2014+1)+1}$
=$\frac{201{4}^{2}}{201{4}^{2}-1+1}$
=1;
(3)(2a+b)(a-2b)-(8a3b-4ab3)÷2ab
=2a2-3ab-2b2-4a2+2b2
=-2a2-3ab;
(4)3(a+1)2-5(a+1)(a-1)+2(a-1)2
=3a2+6a+3-5a2+5+2a2-4a+2
=2a+10.
点评 本题考查整式的混合运算、实数的运算,解答本题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:选择题
| A. | 函数图象经过点(-2,1) | B. | y随x的增大而减小 | ||
| C. | 函数图象经过第一、三象限 | D. | 不论x取何值,总有y<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
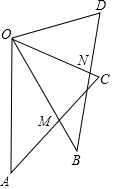 已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.
已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
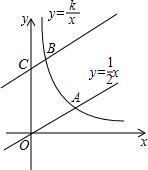 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移4个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,OA=3BC.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移4个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,OA=3BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com