
【题目】如图,直线AB经过x轴上的点M,与反比例函数y= ![]() (x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.
(x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.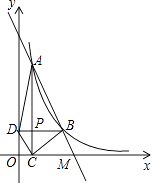
(1)求k的值;
(2)若AB=2BM,求△ABD的面积;
(3)若四边形ABCD为菱形,求直线AB的函数解析式.
【答案】
(1)解:∵A(1,8)在y=![]() 上,
上,
∴k=8.
(2)解:∵A(1,8),B(m,n),
∴AP=8﹣n,AC=8,
∵AB=2BM,
∴ ![]() =
=![]() ,
,
∵AC⊥x轴,BD⊥y轴,
∴BP∥CM,
∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴n=![]() ,
,
把B(m,![]() )代入反比例函数解析式可得m=3,
)代入反比例函数解析式可得m=3,
∴BD=3,
∴S△ABD=![]() BD·AP=
BD·AP=![]() ×3×(8﹣
×3×(8﹣![]() )=8;
)=8;
(3)解:∵四边形ABCD为菱形,
∴BP=DP,
∴点P坐标为(![]() m,n),
m,n),
∵PA=PC,
∴P(1,4),
∴ ![]() m=1,n=4,
m=1,n=4,
∴m=2,n=4,
∴B(2,4),
设直线AB解析式为y=sx+b,
![]() ,
,
∴![]() ,
,
∴直线AB的解析式为y=﹣4x+12.
【解析】(1)将点A(1,8)坐标代入y=![]() 即可得出k值.
即可得出k值.
(2)解:根据A(1,8),B(m,n),得出 ![]() =
=![]() ,由BP∥CM得
,由BP∥CM得![]() =
=![]() =
=![]() ,从而求出n=
,从而求出n=![]() ,将点B(m,
,将点B(m,![]() )代入反比例函数解析式可得m=3,即BD=3,再根据S△ABD=
)代入反比例函数解析式可得m=3,即BD=3,再根据S△ABD=![]() BD·AP即可得出答案.
BD·AP即可得出答案.
(3)由菱形性质得BP=DP,即得点P(![]() m,n),由等腰三角形性质得P(1,4),从而求出m=2,n=4,即B(2,4);再根据待定系数法求出
m,n),由等腰三角形性质得P(1,4),从而求出m=2,n=4,即B(2,4);再根据待定系数法求出
直线AB解析式.
【考点精析】根据题目的已知条件,利用确定一次函数的表达式和三角形的面积的相关知识可以得到问题的答案,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高.


科目:初中数学 来源: 题型:
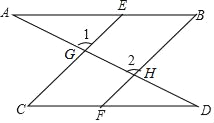
【题目】如图,一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A,G,D,H且∠1=∠2,∠B=∠C
(1)找出图中相互平行的线,说说它们之间为什么是平行的;
(2)证明:∠A=∠D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( ) 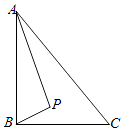
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我东海舰队的一艘军舰在海面A处巡逻时发现一艘不明国籍的船只在C处游弋,立即通知在B处的另一艘军舰一起向其包抄,此时B在A的南偏西30°方向,我两艘军舰分别测得C在A的南偏东75°方向和C在B的北偏东75°方向,已知A,B之间的距离是30海里,求此刻我两艘军舰所在地A,B与C的距离.(结果保留根号)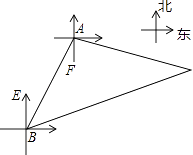
查看答案和解析>>
科目:初中数学 来源: 题型:
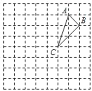
【题目】已知:如图,在边长为1的小正方形网格中,△ABC的顶点都在格点上,建立适当的平面直角坐标系xOy,使得点A、B的坐标分别为(2,3)、(3,2).
(1)在网格中画出满足要求的平面直角坐标系,写出点C的坐标为 ;
(2)若点P是x轴上的一个动点,则PA+PB的最小值为 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
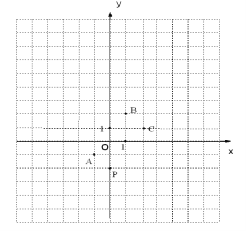
【题目】如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,….如此下去。
(1)在图中画出点M、N,并写出点M、N的坐标:
(2)求经过第2010次跳动之后,棋子落点的位置。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E. 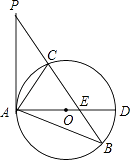
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点C,若ACAB=12,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( ) 
A.5πcm2
B.10πcm2
C.15πcm2
D.20πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )
A.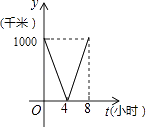
B.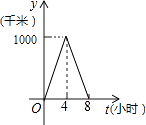
C.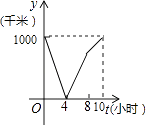
D.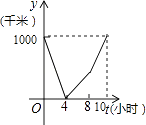
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com