Question

对于点O、M，点M沿MO的方向运动到O左转弯继续运动到N，使OM=ON，且OM⊥ON，这一过程称为M点关于O点完成一次“左转弯运动”．正方形ABCD和点P，P点关于A左转弯运动到P₁，P₁关于B左转弯运动到P₂，P₂关于C左转弯运动到P₃，P₃关于D左转弯运动到P₄，P₄关于A左转弯运动到P₅，…．
（1）请你在图中用直尺和圆规在图中确定点P₁的位置；
（2）连接P₁A、P₁B，判断△ABP₁与△ADP之间有怎样的关系？并说明理由．
（3）以D为原点、直线AD为y轴建立直角坐标系，并且已知点B在第二象限，A、P两点的坐标为（0，4）、（1，1），请你推断：P₄、P₂₀₀₉、P₂₀₁₀三点的坐标．

Answer 1

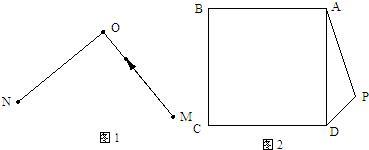
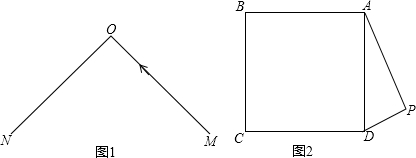
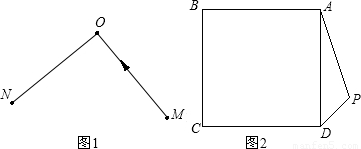
解：（1）用直尺和圆规作图，作图痕迹清晰；

（2）△ABP₁≌△ADP，且△ABP₁可看成是由△ADP绕点A顺时针旋转90°而得．
理由如下：在△ABP₁和△ADP中，
由题意：AB=AD，AP=AP₁，∠PAD=∠P₁AB，
∴△ABP₁≌△ADP，
又∵△ABP₁和△ADP有公共顶点A，且∠PAP₁=90°，
∴△ABP₁可看成是由△ADP绕点A顺时针旋转90°而得；

（3）点P（1，1）关于点A（0，4）左转弯运动到P₁（-3，3），
点P₁（-3，3）关于点B（-4，4）左转弯运动到点P₂（-5，3），
点P₂（-5，3）关于点C（-4，0）左转弯运动到点P₃（-1，1），
点P₃（-1，1）关于点D（0，0）左转弯运动到点P₄（1，1），
点P₄（1，1）关于点A（0，4）左转弯运动到点P₅（-3，3），
点P₅与点P₁重合，点P₆与点P₂重合，点P₂₀₀₉的坐标为（-3，3）
点P₂₀₁₀的坐标为（-5，3）．
分析：（1）根据旋转的性质与“左转弯运动”的定义，即可知首先作∠BAP₁=∠DAP，然后截取AP₁=AP即可求得P₁；
（2）由旋转的性质，即可得AB=AD，AP=AP₁，∠PAD=∠P₁AB，则可证得△ABP₁≌△ADP，又由△ABP₁和△ADP有公共顶点A，且∠PAP₁=90°，即可得△ABP₁可看成是由△ADP绕点A顺时针旋转90°而得；
（3）由题意，即可求得P₁，P₂，P₃，P₄的坐标，即可得规律：各点的坐标每四次一循环，即可求得P₄、P₂₀₀₉、P₂₀₁₀三点的坐标．
点评：此题考查了旋转的性质，全等三角形的判定．此题考查了学生的动手能力，此题难度适中，解题的关键是注意数形结合思想的应用与找到规律：各点的坐标每四次一循环．