
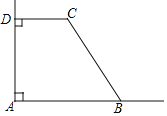
【题目】如图所示,AB⊥AD于点A,CD⊥AD于点D,∠C=120°.若线段BC与CD的和为12,则四边形ABCD的面积可能是( )
A.24![]() B.30
B.30![]() C.45D.
C.45D.![]()
【答案】A
【解析】
过C作CH⊥AB于H,推出四边形ADCH是矩形,四边形ABCD是直角梯形,求得∠BCH=30°,设BC=x,则CD=12﹣x,得到AH=12﹣x,BH=![]() x,CH=
x,CH=![]() x,根据梯形的面积公式和二次函数的性质即可得到结论.
x,根据梯形的面积公式和二次函数的性质即可得到结论.
解:过C作CH⊥AB于H,

∵AB⊥AD,CD⊥AD,
∴∠A=∠ADC=∠AHC=90°,CD∥AB,
∴四边形ADCH是矩形,四边形ABCD是直角梯形,
∴∠DCH=90°,CD=AH,
∵∠BCD=120°,
∴∠BCH=30°,
设BC=x,则CD=12﹣x,
∴AH=12﹣x,BH=![]() x,CH=
x,CH=![]() x,
x,
∴四边形ABCD的面积=![]() (CD+AB)CH=
(CD+AB)CH=![]() (12﹣x+12﹣x+
(12﹣x+12﹣x+![]() x)×
x)×![]() x,
x,
∴四边形ABCD的面积=﹣![]() (x﹣8)2+24
(x﹣8)2+24![]() ,
,
∴当x=8时,四边形ABCD的面积有最大值24![]() ,
,
即四边形ABCD的面积可能是24![]() ,
,
故选:A.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践及创客空间,致力于从小培养学生的创新精神和创造能力,某校开设了“3D”打印,数学编程,智能机器人,陶艺制作,这四门创客课程,为了了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成如下的统计图表:
创客课程 | 频数 | 频率 |
“3D”打印 | 36 | 0.45 |
数学编程 | 0.25 | |
智能机器人 | 16 | b |
陶艺制作 | 8 | |
合计 | a | 1 |

根据图表中提供的信息回答下列问题:
(1)统计表中的a=________,b=________;
(2)“陶艺制作”对应扇形的圆心角度数为________;
(3)若该校有学生2000人,请估算全校喜爱“智能机器人”的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.
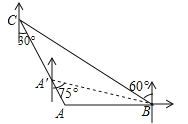
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越野自行车是中学生喜爱的交通工具,市场巨大,竟争也激烈.某品牌经销商经营的![]() 型车去年销售总额为
型车去年销售总额为![]() 万元,今年每辆售价比去年降低
万元,今年每辆售价比去年降低![]() 元,若卖出的数量相同,销售总额将比去年减少
元,若卖出的数量相同,销售总额将比去年减少![]() .
.
(1)设今年![]() 型车每辆销售价为
型车每辆销售价为![]() 元,求
元,求![]() 的值;
的值;
(2)该品牌经销商计划新进一批![]() 型车和新款
型车和新款![]() 型车共
型车共![]() 辆,且
辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,请问应如何安排两种型号车的进货数量,才能使这批售出后获利最多?
型车数量的两倍,请问应如何安排两种型号车的进货数量,才能使这批售出后获利最多?
![]() 、
、![]() 两种型号车今年的进货和销售价格表
两种型号车今年的进货和销售价格表
|
| |
进货价 |
|
|
销售价 |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴正半轴交于点
轴正半轴交于点![]() ,平行于
,平行于![]() 轴的直线
轴的直线![]() 与该抛物线交于
与该抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 位于点
位于点![]() 左侧),与抛物线对称轴交于点
左侧),与抛物线对称轴交于点![]() .
.
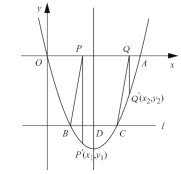
(1)求![]() 的值;
的值;
(2)设![]() 、
、![]() 是
是![]() 轴上的点(点
轴上的点(点![]() 位于点
位于点![]() 左侧),四边形
左侧),四边形![]() 为平行四边形.过点
为平行四边形.过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,与抛物线交于点
轴的垂线,与抛物线交于点![]() 、
、![]() .若
.若![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
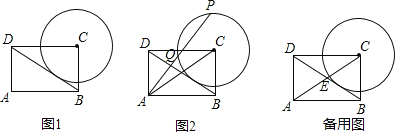
【题目】已知在矩形ABCD中,AB=4,AD=3,⊙C与对角线BD相切.
(1)如图1,求⊙C的半径;
(2)如图2,点P是⊙C上一个动点,连接AP,AC,AP交⊙C于点Q,若sin∠PAC=![]() ,求∠CPA的度数和弧PQ的长;
,求∠CPA的度数和弧PQ的长;
(3)如图,对角线AC与⊙C交于点E,点P是⊙C上一个动点,设点P到直线AC的距离为d,当0<d≤![]() 时,请直接写出∠PCE度数的取值范围.
时,请直接写出∠PCE度数的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顶点为D的抛物线y=﹣x2+bx+c交x轴于A、B(3,0),交y轴于点C,直线y=﹣![]() x+m经过点C,交x轴于E(4,0).
x+m经过点C,交x轴于E(4,0).
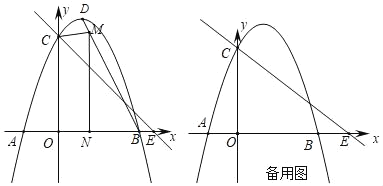
(1)求出抛物线的解析式;
(2)如图1,点M为线段BD上不与B、D重合的一个动点,过点M作x轴的垂线,垂足为N,设点M的横坐标为x,四边形OCMN的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点P为x轴的正半轴上一个动点,过P作x轴的垂线,交直线y=﹣![]() x+m于G,交抛物线于H,连接CH,将△CGH沿CH翻折,若点G的对应点F恰好落在y轴上时,请直接写出点P的坐标.
x+m于G,交抛物线于H,连接CH,将△CGH沿CH翻折,若点G的对应点F恰好落在y轴上时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,根据测试成绩(成绩都不低于50分)绘制出如图所示的部分频数分布直方图.
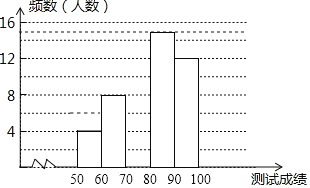
请根据图中信息完成下列各题.
(1)将频数分布直方图补充完整人数;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少;
(3)现将从包括小明和小强在内的4名成绩优异的同学中随机选取两名参加市级比赛,求小明与小强同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
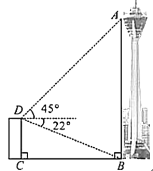
【题目】成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台![]() 处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶
处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶![]() 处测得塔
处测得塔![]() 处的仰角为45°,塔底部
处的仰角为45°,塔底部![]() 处的俯角为22°.已知建筑物的高
处的俯角为22°.已知建筑物的高![]() 约为61米,请计算观景台的高
约为61米,请计算观景台的高![]() 的值.
的值.
(结果精确到1米;参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com