Question

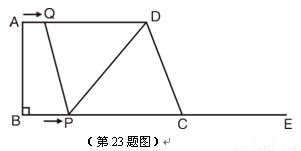
如图，在梯形ABCD中，AD∥BC，∠B＝90°，AD＝16cm，AB＝12cm，BC＝21cm，动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间为t(秒)．

（1）当t为何值时，四边形PQDC是平行四边形．

（2）当t为何值时，以C，D，Q，P为顶点的梯形面积等于60cm²？

（3）是否存在点P，使△PQD是等腰三角形？若存在，请求出所有满足要求的t的值，若不存在，请说明理由．

 

Answer 1

【答案】

（1）∵四边形PQDC是平行四边形

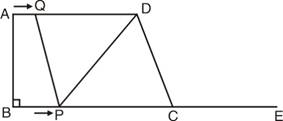
∴DQ=CP

∵DQ=AD－AQ=16－t，CP=21－2t

∴16－t=21－2t

 解得 t=5

当 t=5秒时，四边形PQDC是平行四边形

…………（4分）

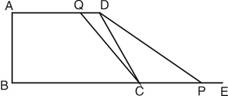
   （2）若点P，Q在BC，AD上时

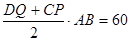         即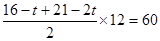

        解得t＝9（秒）  …………（2分）

        若点P在BC延长线上时，则CP=2t-21,

∴

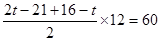
        解得 t＝15（秒）

  ∴当t＝9或15秒时，以C，D，Q，P为顶点的梯形面积等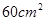（2分）

  （3）当PQ＝PD时

     作PH⊥AD于H，则HQ=HD

     ∵QH=H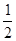D=QD=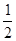（16-t）

     由AH=BP得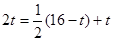 

     解得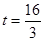秒  …………（2分）

     当PQ=QD时  QH=AH－AQ=BP－AQ＝2t－t=t, QD=16-t

     ∵QD²= PQ²=12²+t²

∴（16--t）²=12²+t²  解得(秒) …………（2分）

     当QD=PD时  DH=AD -AH=AD-BP=16-2t

     ∵QD²=PD²=PH²+HD²=12²+(16-2t)²

∴(16-t)²=12²+(16-2t)²

即  3t²-32t+144=0

∵△＜0

∴方程无实根

综上可知,当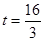秒或(秒)时, △BPQ是等腰三角形……（2分）

【解析】（1）由题意已知，AD∥BC，要使四边形PQDC是平行四边形，则只需要让QD=PC即可，因为Q、P点的速度

已知，AD、BC的长度已知，要求时间，用时间=路程÷速度，即可求出时间；

（2）要使以C、D、Q、P为顶点的梯形面积等于60cm²，可以分为两种情况，即点P、Q在BC、AD，点P在

BC延长线上，再利用梯形面积公式，即（QD+PC）×AB÷2=60，因为Q、P点的速度已知，AD、AB、

BC的长度已知，用t可分别表示QD、BC的长，即可求得时间t；

（3）使△PQD是等腰三角形，可分三种情况，即PQ=PD、PQ=QD、QD=PD；可利用等腰三角形及直角梯形的

性质，分别用t表达等腰三角形的两腰长，再利用两腰相等即可求得时间t．