
【题目】如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为144,则BE________
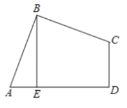
【答案】12
【解析】
作BF⊥CD交CD的延长线于点F,由已知条件可证得∠ABE=∠CBF,且由已知∠AEB=∠CFB=90°,AB=BC,所以△ABE≌△CBF,可得BE=BF,四边形ABCD的面积等于新正方形FBED的面积,即可得BE长.
过B点作BF⊥CD,与DC的延长线交于F点,则∠F=90°,

∵BE⊥AD,∴∠AEB=∠BED=90°,
又∵∠CDA=90°,
∴四边形BEDF是矩形,
∴∠EBF=90°,
∵∠ABC=90°,
∴∠ABE+∠EBC=∠CBF+∠EBC,
∴∠ABE=∠CBF,
又AB=BC,
∴△ABE≌△CBF,
∴BE=BF,
∴矩形BEDF为正方形,
∴S正方形BEDF=S△BCF+S四边形BEDC= S△BAE+S四边形BEDC=S四边形ABCD=144,
∴BE2=144,
∴BE=12,
故答案为:12.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场服装部销售一种名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价
元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价![]() 元时,平均每天可多卖出
元时,平均每天可多卖出![]() 件.
件.
(1)若商场要求该服装部每天盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多.
查看答案和解析>>
科目:初中数学 来源: 题型:
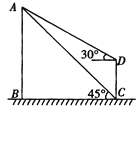
【题目】为了测量某风景区内一座塔AB的高度,某人分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度。(结果精确到0.1m)(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
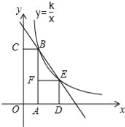
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y=![]() 的图象上,OA=2,OC=6,则正方形ADEF的边长为______.
的图象上,OA=2,OC=6,则正方形ADEF的边长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB⊥直线l于点B,点M在直线l上,分别以AB、AM为边作等边△ABC和等边△AMN,直线CN交直线l于点D.
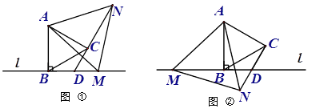
(1)当点M在AB右侧时,如图①,试探索线段CN、CD、DM的数量关系,并说明理由;
(2)当点M在AB左侧时,如图②,(1)中线段CN、CD、DM的数量关系仍然成立吗?若不成立,写出新的数量关系;
(3)若BM=2BD,DN=9,则CD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段AB上取一点C(非中点),分别以AC、BC为边在AB的同侧作等边△ACD和等边△BCE,连接AE交CD于点F,连接BD交CE于点G,AE和BD交于点H.
(1)求证:△ACE≌△DCB
(2)求∠BHE的度数

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( )
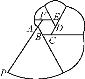
A. 13π cm B. 14π cm C. 15π cm D. 16π cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ED为☉O的直径且ED=4,点A(不与点E,D重合)为☉O上一个动点,线段AB经过点E,且EA=EB,F为☉O上一点,∠FEB=90°,BF的延长线交AD的延长线于点C.
(1)求证:△EFB≌△ADE;
(2)当点A在☉O上移动时,直接回答四边形FCDE的最大面积为多少.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,E、F分别是正方形AD、CD边上的点,且∠EBF=45°,对角线AC交BE,BF于M,N,对于以下结论,正确的是( )①AE+CF=FE②△ABE≌△BCF③AM2+CN2=MN2④△EFD的周长等于2AB

A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com