

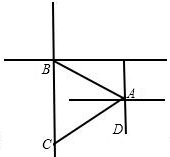
 解:(1)如图,灯塔A在灯塔B的南偏东60°方向上,即∠CBA=60°,
解:(1)如图,灯塔A在灯塔B的南偏东60°方向上,即∠CBA=60°,

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
 28、(1)灯塔A在灯塔B的南偏东60°方向上,A、B相距30海里,轮船C在B的正南方向,在灯塔A的南偏西60°方向上,通过画图(用1个单位代表10海里)确定轮船C的位置,求∠BAC和∠ACB的度数,并求出轮船C与灯塔B的距离.
28、(1)灯塔A在灯塔B的南偏东60°方向上,A、B相距30海里,轮船C在B的正南方向,在灯塔A的南偏西60°方向上,通过画图(用1个单位代表10海里)确定轮船C的位置,求∠BAC和∠ACB的度数,并求出轮船C与灯塔B的距离.查看答案和解析>>
科目:初中数学 来源: 题型:
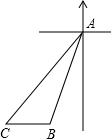 如图,一船在A处看见灯塔B在它的南偏西30°的方向,这时船和灯塔的距离为40海里,然后船向西南方向船行到C处,这时望见灯塔B在它的正东方向,问船航行了多少海里?(不取近似值)
如图,一船在A处看见灯塔B在它的南偏西30°的方向,这时船和灯塔的距离为40海里,然后船向西南方向船行到C处,这时望见灯塔B在它的正东方向,问船航行了多少海里?(不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:
 23、(1)如图,把推理的根据填在括号内:
23、(1)如图,把推理的根据填在括号内:查看答案和解析>>
科目:初中数学 来源: 题型:
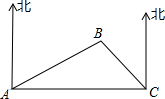 暑假里,吴鹏和爸爸妈妈一起进行了海上旅游.上午八点时游船在A处(如图),他们看见灯塔B在游船的北偏东50°方向,游船以5海里/小时的时速向正东方向行驶,上午十点时游船行驶到C处,他们发现此时灯塔B在海船的西北方向,请求出此时灯塔B到C处的距离.(友情提示:以下数据可以选用:sin40°≈0.6428,cos40°≈0.7660,tan40°≈0.8391,
暑假里,吴鹏和爸爸妈妈一起进行了海上旅游.上午八点时游船在A处(如图),他们看见灯塔B在游船的北偏东50°方向,游船以5海里/小时的时速向正东方向行驶,上午十点时游船行驶到C处,他们发现此时灯塔B在海船的西北方向,请求出此时灯塔B到C处的距离.(友情提示:以下数据可以选用:sin40°≈0.6428,cos40°≈0.7660,tan40°≈0.8391,| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com