
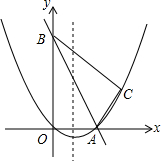
 如图,在平面直角坐标系中,直线y=-2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
如图,在平面直角坐标系中,直线y=-2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.分析 (1)先确定出点A,B坐标,再用待定系数法求出抛物线解析式;用勾股定理逆定理判断出△ABC是直角三角形;
(2)根据运动表示出OP=2t,CQ=10-t,判断出Rt△AOP≌Rt△ACQ,得到OP=CQ即可;
(3)分三种情况用平面坐标系内,两点间的距离公式计算即可,
解答 解:(1)∵直线y=-2x+10与x轴,y轴相交于A,B两点,
∴A(5,0),B(0,10),
∵抛物线过原点,
∴设抛物线解析式为y=ax2+bx,
∵抛物线过点A(5,0),C(8,4),
∴$\left\{\begin{array}{l}{25a+5b=0}\\{64a+8b=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=\frac{1}{6}}\\{b=-\frac{5}{6}}\end{array}\right.$,
∴抛物线解析式为y=$\frac{1}{6}$x2-$\frac{5}{6}$x,
∵A(5,0),B(0,10),C(8,4),
∴AB2=52+102=125,BC2=82+(10-4)2=100,AC2=42+(8-5)2=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
(2)如图1,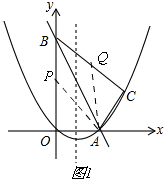
当P,Q运动t秒,即OP=2t,CQ=10-t时,
由(1)得,AC=OA,∠ACQ=∠AOP=90°,
在Rt△AOP和Rt△ACQ中,
$\left\{\begin{array}{l}{AC=OA}\\{PA=QA}\end{array}\right.$,
∴Rt△AOP≌Rt△ACQ,
∴OP=CQ,
∴2t=10-t,
∴t=$\frac{10}{3}$,
∴当运动时间为$\frac{10}{3}$时,PA=QA;
(3)存在,
∵y=$\frac{1}{6}$x2-$\frac{5}{6}$x,
∴抛物线的对称轴为x=$\frac{5}{2}$,
∵A(5,0),B(0,10),
∴AB=5$\sqrt{5}$
设点M($\frac{5}{2}$,m),
①若BM=BA时,
∴($\frac{5}{2}$)2+(m-10)2=125,
∴m1=$\frac{20+5\sqrt{19}}{2}$,m2=$\frac{20-5\sqrt{19}}{2}$,
∴M1($\frac{5}{2}$,$\frac{20+5\sqrt{19}}{2}$),M2($\frac{5}{2}$,$\frac{20-5\sqrt{19}}{2}$),
②若AM=AB时,
∴($\frac{5}{2}$)2+m2=125,
∴m3=$\frac{5\sqrt{19}}{2}$,m4=-$\frac{5\sqrt{19}}{2}$,
∴M3($\frac{5}{2}$,$\frac{5\sqrt{19}}{2}$),M4($\frac{5}{2}$,-$\frac{5\sqrt{19}}{2}$),
③若MA=MB时,
∴($\frac{5}{2}$-5)2+m2=($\frac{5}{2}$)2+(10-m)2,
∴m=5,
∴M($\frac{5}{2}$,5),此时点M恰好是线段AB的中点,构不成三角形,舍去,
∴点M的坐标为:M1($\frac{5}{2}$,$\frac{20+5\sqrt{19}}{2}$),M2($\frac{5}{2}$,$\frac{20-5\sqrt{19}}{2}$),M3($\frac{5}{2}$,$\frac{5\sqrt{19}}{2}$),M4($\frac{5}{2}$,-$\frac{5\sqrt{19}}{2}$),
点评 此题是二次函数综合题,主要考查了待定系数法求函数解析式,三角形的全等的性质和判定,等腰三角形的性质,解本题的关键是分情况讨论,也是本题的难点.


科目:初中数学 来源: 题型:选择题
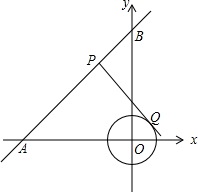 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{119}}{5}$ | C. | 2.4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
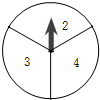 商场为了促销某件商品,设置了如图的一个转盘,它被分成了3个相同的扇形.各扇形分别标有数字2,3,4,指针的位置固定,该商品的价格由顾客自由转动此转盘两次来获取,每次转动后让其自由停止,记下指针所指的数字(指针指向两个扇形的交线时,当作右边的扇形),先记的数字作为价格的十位数字,后记的数字作为价格的个位数字,则顾客购买商品的价格不超过30元的概率是多少?
商场为了促销某件商品,设置了如图的一个转盘,它被分成了3个相同的扇形.各扇形分别标有数字2,3,4,指针的位置固定,该商品的价格由顾客自由转动此转盘两次来获取,每次转动后让其自由停止,记下指针所指的数字(指针指向两个扇形的交线时,当作右边的扇形),先记的数字作为价格的十位数字,后记的数字作为价格的个位数字,则顾客购买商品的价格不超过30元的概率是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
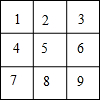 如图,九个小朋友用抽签的方式来确定各自的座位(如图中1~9这9个座位),小明第一个抽,抽到6号座位,小华第二个抽,那么小华抽到的座位恰好和小明的座位相邻的概率是$\frac{3}{8}$.
如图,九个小朋友用抽签的方式来确定各自的座位(如图中1~9这9个座位),小明第一个抽,抽到6号座位,小华第二个抽,那么小华抽到的座位恰好和小明的座位相邻的概率是$\frac{3}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
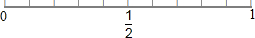 将下列事件发生的概率填在图中:(只填各事件的序号)
将下列事件发生的概率填在图中:(只填各事件的序号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com