
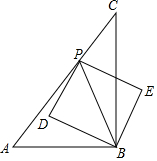
 ���壬����һ���߶�Ϊ�Խ����������Σ���Ƹ�������Ϊ�����߶εġ��Խ��������Ρ�����ͼ���ڡ�ABC�У���ABC=90�㣬AB=3cm��BC=4cm����P�ӵ�C������������CA-AB��5cm/s���ٶ��˶�������P���B���غ�ʱ�����߶�PB�ġ��Խ��������Ρ������P���˶�ʱ��Ϊt��s�����߶�PB�ġ��Խ��������Ρ������ΪS��cm2����
���壬����һ���߶�Ϊ�Խ����������Σ���Ƹ�������Ϊ�����߶εġ��Խ��������Ρ�����ͼ���ڡ�ABC�У���ABC=90�㣬AB=3cm��BC=4cm����P�ӵ�C������������CA-AB��5cm/s���ٶ��˶�������P���B���غ�ʱ�����߶�PB�ġ��Խ��������Ρ������P���˶�ʱ��Ϊt��s�����߶�PB�ġ��Խ��������Ρ������ΪS��cm2�������� ��1��t=0ʱ�������εĶԽ���Ϊ4���ɴ˼�����������
��2����ͼ1�У����߶�PB�ġ��Խ��������Ρ�������ͬʱ���ڡ�ABC�ı���ʱ���������εı߳�Ϊx����PE��AB���ɵ�$\frac{PE}{AB}$=$\frac{CE}{CB}$����$\frac{x}{3}$=$\frac{4-x}{4}$�����x=$\frac{12}{7}$�������PC�ij����ɽ�����⣮
��3�����������ηֱ�������ͼ2�У���0��t��1ʱ����PH��BC��H�����PB2���ɣ�����ͼ3�У���1��t��$\frac{8}{5}$ʱ�����PB2���ɣ�
��4���������������ۢ���ͼ4�У���D��E�ڡ�BAC��ƽ������ʱ���ڵ���P�˶�����Aʱ��������������ʱt=1s������ͼ5�У�����E�ڡ�BAC�Ľ�ƽ������ʱ���ֱ���⼴�ɣ�
��� �⣺��1��t=0ʱ��������PEBD�ĶԽ���ΪPB��BC�غϣ�PB=BC=4��S=$\frac{1}{2}$•4•4=8��
�ʴ�Ϊ8��
��2����ͼ1�У����߶�PB�ġ��Խ��������Ρ�������ͬʱ���ڡ�ABC�ı���ʱ���������εı߳�Ϊx��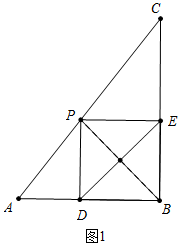
��PE��AB��
��$\frac{PE}{AB}$=$\frac{CE}{CB}$��
��$\frac{x}{3}$=$\frac{4-x}{4}$��
���x=$\frac{12}{7}$��
��PE=$\frac{12}{7}$��CE=4-$\frac{12}{7}$=$\frac{16}{7}$��
��PC=$\sqrt{P{E}^{2}+E{C}^{2}}$=$\frac{20}{7}$��
��t=$\frac{\frac{20}{7}}{5}$=$\frac{4}{7}$s��
��3������ͼ2�У���0��t��1ʱ����PH��BC��H��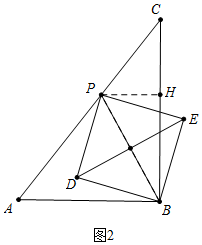
��PC=5t����HC=4t��PH=3t��
��Rt��PHB��PB2=PH2+BH2=��3t��2+��4-4t��2=25t2-32t+16��
��S=$\frac{1}{2}$PB2=$\frac{25}{2}$t2-16t+8��
����ͼ3�У���1��t��$\frac{8}{5}$ʱ��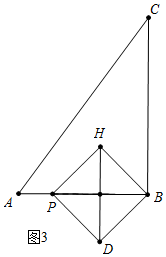
��PB=8-5t��
��S=$\frac{1}{2}$PB2=$\frac{25}{2}$t2-40t+32��
����������S=$\left\{\begin{array}{l}{\frac{25}{2}{t}^{2}-16t+8}&{��0��t��1��}\\{\frac{25}{2}{t}^{2}-40t+32}&{��1��t��\frac{8}{5}��}\end{array}\right.$��
��4������ͼ4�У���D��E�ڡ�BAC��ƽ������ʱ����֪AB=AP=3��PC=2����t=$\frac{2}{5}$s��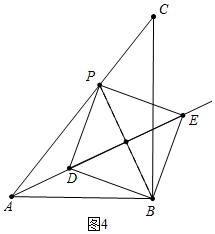
�ڵ���P�˶�����Aʱ��������������ʱt=1s��
����ͼ5�У�����E�ڡ�BAC�Ľ�ƽ������ʱ����EH��BC��H��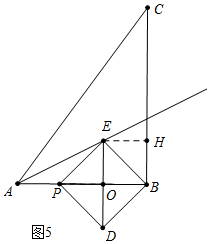
��֪EBƽ�֡�ABC��
���E�ǡ�ABC�����ģ��ı���EOBH�������Σ�OB=EH=EO=BH=$\frac{AB+BC-AB}{2}$=1��ֱ������������Բ�뾶��ʽ����
��PB=2OB=2��
��AP=1��
��t=$\frac{6}{5}$s��
�����������������˶������У����߶�PB�ġ��Խ��������Ρ�������һ���������ڡ�CAB��ƽ������ʱ��t��ֵΪ$\frac{2}{5}$s ��1s��$\frac{6}{5}$s��
���� ���⿼���ı����ۺ��⡢�����ε����ʡ���ƽ���ߵĶ��塢���ɶ���ֱ�������ε�����Բ�뾶��ƽ���ߵ����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
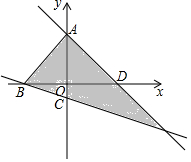 ��ƽ��ֱ������ϵ�У���A��B��C��D���������ϵĵ��ҵ�C�����ǣ�0��-1����AB=5���㣨a��b������ͼ��ʾ����Ӱ�����ڲ����������߽磩����֪OA=OD=4����a��ȡֵ��Χ�ǣ�������
��ƽ��ֱ������ϵ�У���A��B��C��D���������ϵĵ��ҵ�C�����ǣ�0��-1����AB=5���㣨a��b������ͼ��ʾ����Ӱ�����ڲ����������߽磩����֪OA=OD=4����a��ȡֵ��Χ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ab��2=a2b2 | B�� | 2a-a=2 | C�� | a2+a2=a4 | D�� | ��a2��3=a5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 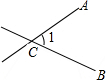 | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
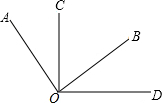 ��ͼ����AOB=��COD=90��
��ͼ����AOB=��COD=90���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com