
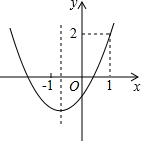 已知抛物线y=ax2+bx+c的图象如图所示.
已知抛物线y=ax2+bx+c的图象如图所示.分析 由二次函数的图象,很容易判断a、b、c的符号,根据图象与x轴有两个交点,知道b2-4ac>0;由图象可知a-b+c的符号与a+b+c的值;再根据图象和a、b、c之间的关系进行巧妙变换得到(3)中结论正确与否.
解答 解:(1)∵图象开口向上∴a>0;
∵-$\frac{b}{2a}$<0,a>0∴b>0;
∵图象与y轴交于负半轴∴c<0;
∵图象与x轴有两个交点∴b2-4ac>0;
令x=-1,则y=a-b+c,由图象可知,x=-1时,y<0,故a-b+c<0.
由上可知:a>0,b>0,c<0,b2-4ac>0,a-b+c<0.
(2)令x=1,则y=a+b+c,由图象可知,x=1时,y=2,故a+b+c=2.
(3)∵a-b+c<0,a+b+c=2
∴a+c<b,a+c=2-b
∴2-b<b
∴b>1,则①错误;
∵-$\frac{b}{2a}$>-1,a>0
∴b<2a,则②正确;
∴a>$\frac{b}{2}$
又∵b>1
∴a>$\frac{1}{2}$,则③正确;
∵a+b+c=2,b>1
∴a+c=2-b<1,则④正确;
∵a+b+c=2,c<0
∴a+b=2-c>2>c
∴,-a-b+c<0,则⑤正确.
故答案为:②③④⑤.
点评 本题考察二次函数的图象与系数之间的关系,会利用图象给出的信息,对一些式子进行判断正误.


科目:初中数学 来源: 题型:解答题
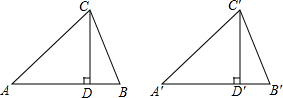 如图,已知在△ABC和△A′B′C′中,CD,C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.求证:△ABC≌△A′B′C′.
如图,已知在△ABC和△A′B′C′中,CD,C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.求证:△ABC≌△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 2次 | B. | 3次 | C. | 4次 | D. | 7次 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
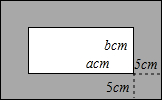 长方形壁画的长为a cm,宽为b cm,现要在其四周镶上宽为5cm的彩条(如图),至少需要多长的彩条才能镶完?所列的式子是否是整式?若是整式,请判断它是单项式还是多项式.
长方形壁画的长为a cm,宽为b cm,现要在其四周镶上宽为5cm的彩条(如图),至少需要多长的彩条才能镶完?所列的式子是否是整式?若是整式,请判断它是单项式还是多项式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
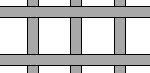 如图,有一块长为30米,宽为10米的长方形菜地,在菜地里要留出南北三条,东西两条,宽度一样的小路,并使实际种植面积为216平方米,求小路的宽应为几米.
如图,有一块长为30米,宽为10米的长方形菜地,在菜地里要留出南北三条,东西两条,宽度一样的小路,并使实际种植面积为216平方米,求小路的宽应为几米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
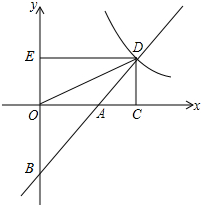 如图,直线y=x+b(b<0)与两坐标轴分别交于A,B两点,与双曲线y=$\frac{2}{x}(x>0)$交于点D,过点D作两坐标轴的垂线DC,DE,连结OD.
如图,直线y=x+b(b<0)与两坐标轴分别交于A,B两点,与双曲线y=$\frac{2}{x}(x>0)$交于点D,过点D作两坐标轴的垂线DC,DE,连结OD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com