
| A. | $\frac{22}{7}$ | B. | $\sqrt{81}$ | C. | π-3.14 | D. | $\sqrt{2}$ |
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
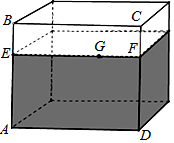 有一个如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处面包屑.
有一个如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处面包屑.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com