
分析 (1)设甲种救灾物品每件的价格是x元,则乙种救灾物品每件的价格是(x-10)元,根据数量=总价÷单价结合用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)根据总价=单价×数量列式计算,即可得出结论.
解答 解:(1)设甲种救灾物品每件的价格是x元,则乙种救灾物品每件的价格是(x-10)元,
根据题意得:$\frac{350}{x}$=$\frac{300}{x-10}$,
解得:x=70,
经检验,x=70是原分式方程的解,
∴x-10=60.
答:甲种救灾物品每件的价格是70元,则乙种救灾物品每件的价格是60元.
(2)70×$\frac{1}{1+3}$×2000+60×$\frac{3}{1+3}$×2000=125000(元).
答:若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金125000元.
点评 本题考查了分式方程的应用,解题的关键是:(1)根据数量=总价÷单价.列出关于x的分式方程;(2)根据总价=单价×数量列式计算.


科目:初中数学 来源: 题型:解答题
 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
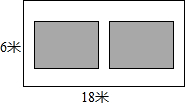 如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为1米.
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为1米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
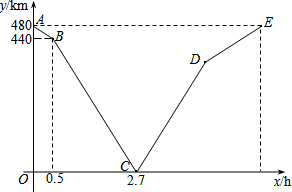 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设一辆车先出发xh后,另一辆车也开始行驶,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设一辆车先出发xh后,另一辆车也开始行驶,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种糖果 | 乙种糖果 | 丙种糖果 | |
| 单价(元/千克) | 15 | 20 | 25 |
| 千克(千克) | 30 | 40 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com