
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据已知条件证明BE=DF,BE∥DF,从而得出四边形DFBE是平行四边形,即可证明DE∥BF,
(2)先证明DE=BE,再根据邻边相等的平行四边形是菱形,从而得出结论.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=![]() AB,DF=
AB,DF=![]() CD.
CD.
∴BE=DF,BE∥DF,
∴四边形DFBE是平行四边形,
∴DE∥BF;
(2)∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DFBE是平行四边形,
∴四边形DEBF是菱形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.

查看答案和解析>>
科目:初中数学 来源: 题型:
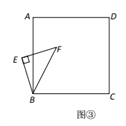
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG且EG⊥CG;
(2)将图①中△BEF绕B点逆时针旋转45,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:(1)AD=CB;(2)AE=CF;(3)∠B=∠D;(4)AD∥BC.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年7月23日,记者从省旅发委获悉,上半年我省实现旅游总收入约2381亿元人民币,该数据用科学记数法表示为( )
A. 2.381×1011元 B. 2.381×1012元 C. 0.2381×1012元 D. 23.81×1010元
查看答案和解析>>
科目:初中数学 来源: 题型:
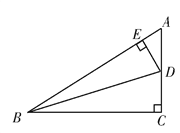
【题目】在Rt△ABC中,BD平分∠ABC, DE⊥AB于E,则:
(1)哪条线段与DE相等?为什么?
(2)若BC=8,AC=6,求BE,AE的长和△AED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,已知符合该规定行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生会准备调查全校七年级学生每天(除课间操外)的课外锻炼时间.
(1)确定调查方式时,甲同学说:“我到1班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到全校七年级每个班去随机调查一定数量的同学”.你认为调查方式最为合理的是 (填“甲”或“乙”或“丙”);
(2)他们采用了最为合理的调查方法收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请根据图1和图2所提供的信息,将图1中的条形统计图补充完整;(注:图2中相邻两虚线形成的圆心角为30°)
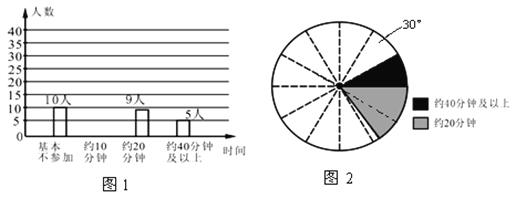
(3)若该校七年级共有1200名同学,请你估计其中每天(除课间操外)课外锻炼时间不大于20分钟的人数,并根据调查情况向学生会提出一条建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com