二次根式$\sqrt{5-x}$中x的取值范围是( )A．x≥5B．x≤5C．x≥-5D．x＜5 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

6．二次根式$\sqrt{5-x}$中x的取值范围是（　　）

A．

x≥5

B．

x≤5

C．

x≥-5

D．

x＜5

分析依据二次根式被开放数为非负数列不等式求解即可．

解答解：由题意得：5-x≥0，
解得：x≤5．
故选B．

点评本题主要考查的是二次根式有意义的条件，熟练掌握二次根式有意义的条件是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

11．

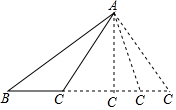如图，△ABC底边BC上的高是6cm．当三角形的顶点C沿底边所在的直线向B运动时，三角形的面积发生变化，如果三角形的底边长为x（cm），三角形的面积y（cm²），那么y与x的关系可以表示为y=3x．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．

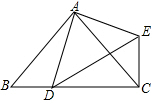如图，在△ABC中，AB=AC，点D在线段BC上运动，连接AD，以AD为边作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
①若tan∠ABC=2，AB=3$\sqrt{5}$，AE=2$\sqrt{10}$，求BD长？
②若直线DE与直线BC所夹锐角的正切值是$\frac{\sqrt{2}}{3}$，cos∠BAC=$\frac{1}{3}$，BC=4，求BD的长．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

14．

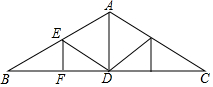如图是屋顶的“人字形”钢架，其中斜梁AB=AC，顶角∠BAC=120°，立柱AD⊥BC，EF⊥BC，DE∥AC，AB=8m，则EF=2m．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

1．a、b、c是三角形的三边长，且（a+b）²=c²+2ab，则这个三角形是（　　）

A．

锐角三角形

B．

直角三角形

C．

钝角三角形

D．

等边三角形

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

11．在π，$\frac{17}{8}$，-$\sqrt{7}$，$\root{3}{125}$，3.1415，0.3，-$\frac{{\sqrt{5}}}{3}$，-3.20202020…，4.1818818881…中，有理数的个数有（　　）

A．

4个

B．

5个

C．

6个

D．

7个

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

18．下列运算中，错误的个数为（　　）
①$\sqrt{1\frac{25}{144}}$=1$\frac{5}{12}$；②$\sqrt{（-4）^{2}}$=±4；③$\sqrt{-{2}^{2}}$=-$\sqrt{{2}^{2}}$；④$\sqrt{\frac{1}{16}+\frac{1}{4}}$=$\frac{1}{4}$+$\frac{1}{2}$=$\frac{3}{4}$．

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．

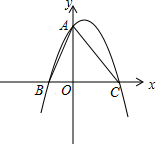如图，在平面直角坐标系中，二次函数y=-x²+x+6的图象与y轴交于点A，与x轴交于B，C两点（点B在点C的左侧），连接AB，AC．
（1）①点B的坐标为（-2，0），点C的坐标为（3，0），AC的长为3$\sqrt{5}$；
②求∠BAC的正弦值
（2）将△AOB沿直线AB折叠得到△AEB，将△AOC沿直线AC折叠得到△AFC，分别延长EB，FC相交于点H
①点H坐标为（$\frac{6}{5}$，-$\frac{12}{5}$），点H不在抛物线对称轴上（“在”或“不在”）
②连接EF，将∠BAC绕点A顺时针旋转，射线AB旋转后交线段EH于点B′，交线段EF于点M，射线AC旋转后交线段FH于点C′，交线段EF于点N，当B′H²+C′H²=33时，MN的长度为$\frac{\sqrt{66}}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．某校将周五上午大课间活动项目定为跳绳活动，为此学校准备购置长、短两种跳绳若干．已知长跳绳的单价比短跳绳单价的三倍少4元，且购买2条长跳绳与购买5条短跳绳的费用相同．
（1）两种跳绳的单价各是多少元？
（2）若学校准备用不超过1950元的现金购买190条长、短跳绳，且短跳绳的条数不超过长跳绳的5倍，问学校有几种购买方案可供选择？并写出这几种方案．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学