
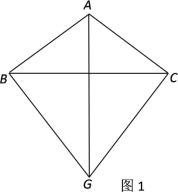
【题目】如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.
(1)求证:直线AG垂直平分BC;
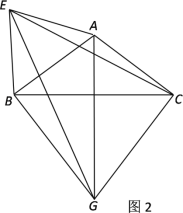
(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.
【答案】(1)证明见解析(2)△EGC构成直角三角形
【解析】
(1)由GB=GC,得出点G在BC的垂直平分线上,同理得出点A在BC的垂直平分线上,即可得出结论;
(2)由等边三角形的性质得出GB=BC=GC, EB=BA,∠EBA=∠GBC=∠BGC=∠BCG =60°,证出∠EBC=∠ABG,由SAS证明△EBC≌△ABG,得出∠ECB=∠AGB,再由等腰三角形的性质即可得出结论.
(1)∵△GBC为等边三角形,∴GB=GC,
∴点G在BC的垂直平分线上,
又∵AB=AC,∴点A在BC的垂直平分线上,
∴直线AG垂直平分BC;
(2)△EGC构成直角三角形,
∵△GBC和△ABE为等边三角形,
∴GB=BC=GC,EB=BA,∠EBA=∠GBC=∠BGC=∠BCG =60°,
∴∠EBC=∠ABG,∴△EBC≌△ABG ,
∴∠ECB=∠AGB,∵GB=GC且AG⊥BC,∴∠AGB=![]() ∠BGC=30°,
∠BGC=30°,
∴∠ECB=30°,
∴∠ECG=90°,即△EGC构成直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )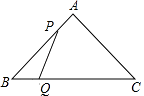
A.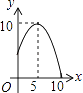
B.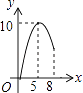
C.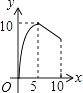
D.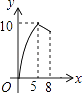
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一根绳子对折成一条线段AB,在线段AB取一点P,使AP=![]() ,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm.
,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
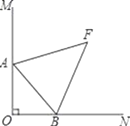
【题目】如图,∠MON=90°,OB=2,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两角平分线所在的直线交于点F,求点A在运动过程中线段BF的最小值为 ______
查看答案和解析>>
科目:初中数学 来源: 题型:
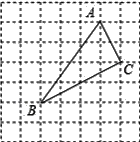
【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(3,4)、C(4,2),则点B的坐标为 ;
(2)图中格点△ABC的面积为 ;
(3)判断格点△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2i=(﹣1)i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4ni=(i4)ni=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为( )
A. 0 B. i C. ﹣1 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
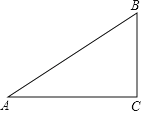
【题目】如图,Rt△ABC中,∠C=90°,AC=8,BC=6.
(1)尺规作图:作△BAC的角平分线AD(保留作图痕迹,不写作法);
(2)求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了了解气温对用电量的影响,对去年自己家的每月用电量和当地气温进行了统计.当地去年每月的平均气温如图1,小明家去年月用电量如图2.
根据统计表,回答问题:
(1)当地去年月平均气温的最高值、最低值各为多少?相应月份的用电量各是多少?
(2)请简单描述月用电量与气温之间的关系;
(3)假设去年小明家用电量是所在社区家庭年用电量的中位数,据此他能否预测今年该社区的年用电量?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b(![]() )与y=-4x(
)与y=-4x(![]() )的图像相交于点P(1,n),且C(3,2)在一次函数图像上
)的图像相交于点P(1,n),且C(3,2)在一次函数图像上
⑴求k、b的值;
⑵直接写出kx+b>-4x的解集
⑶连接OC,求三角形OPC的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com