
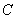 是半圆
是半圆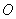 的半径
的半径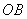 上的动点,作
上的动点,作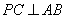 于
于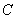 .点
.点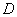 是半圆上位于
是半圆上位于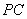 左侧的点,连结
左侧的点,连结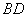 交线段
交线段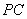 于
于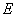 ,且
,且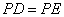 .
.
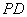 是⊙O的切线.
是⊙O的切线.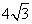 ,
,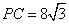 ,设
,设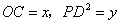 .
.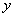 关于
关于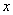 的函数关系式.
的函数关系式.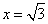 时,求
时,求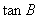 的值.
的值.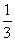
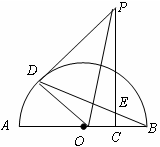
 ,则PO2=y+(4
,则PO2=y+(4 )2=y+48,在Rt△PCO中OC="x" PC=8
)2=y+48,在Rt△PCO中OC="x" PC=8 ,则可得PO2=x2+(8
,则可得PO2=x2+(8 )2=x2+192 ,所以有y+48=x2+192,从而求得结果;
)2=x2+192 ,所以有y+48=x2+192,从而求得结果; 时,可得y=147,即可得到PD、PE的长,由PC=8
时,可得y=147,即可得到PD、PE的长,由PC=8 可得EC的长,又OC=X=
可得EC的长,又OC=X= ,OB=4
,OB=4 可得CB=3
可得CB=3 ,在Rt△BCE中,根据正切函数的定义求解即可.
,在Rt△BCE中,根据正切函数的定义求解即可.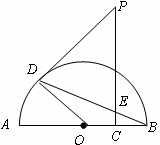

 )2="y+48"
)2="y+48" 
 )2=x2+192
)2=x2+192  时,y=147
时,y=147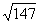 =7
=7


 -7
-7 =
=
 ,OB=4
,OB=4

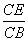 =
=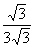 =
=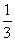 .
.

科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
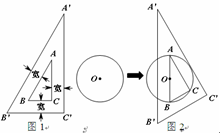
 ,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.
,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.
 ︰2时,求弧AF的度数;
︰2时,求弧AF的度数;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com