
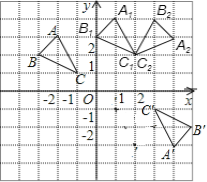
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)画出△A1B1C1绕原点顺时针旋90°后得到 的△A2B2C2;
(3)若△A′B′C′与△ABC是中心对称图形,则对称中心的坐标为 .

【答案】(1)(2)图见解析(3)图见解析,(1,0)
【解析】试题分析:(1)首先将A、B、C三点分别向右平移3个单位,再向上平移1个单位,得A1、B1、C1三点,顺次连接这些点,即可得到所求作的三角形;
(2)找出点B、C绕点A顺时针旋转90°的位置,然后顺次连接即可;
(3)△A′B′C′与△ABC是中心对称图形,连接对应点即可得出答案.
解:(1)将A,B,C,分别右平移3个单位长度,再向上平移1个单位长度,可得出平移后的△A1B1C1;
(2)将△A1B1C1三顶点A1,B1,C1,绕原点旋转90°,即可得出△A2B2C2;
(3)∵△A′B′C′与△ABC是中心对称图形,
连接AA′,BB′CC′可得出交点:(1,0),
故答案为:(1,0).


科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°
,cos22°![]() ,tan22°
,tan22°![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 对载人航天器零部件的检查适合采用抽样调查的方式
B. 某市天气预报中说“明天降雨的概率是80%”,表示明天该市有80%的地区降雨
C. 通过抛掷1枚质地均匀的硬币,确定谁先发球的比赛规则是公平的
D. 掷一枚骰子,点数为3的面朝上是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,![]() =
=![]() ,BE交AD于点F.
,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=![]() ,则AF的长度为( )
,则AF的长度为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把Rt△ABC各边的长度都扩大3倍得到Rt△A′B′C′,对应锐角A,A′的正弦值的关系为( )
A. sinA=3sinA′ B. sinA=sinA′ C. 3sinA=sinA′ D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
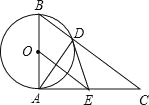
【题目】如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收2.6元(不足1千米按1千米计),某人从甲地到乙地经过的路程是x千米,出租车费为21元,那么x的最大值是( )
A.11
B.8
C.7
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com