
 矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π).
矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π). 分析 先根据旋转的性质得出∠ECD的度数,再结合矩形的性质,求得CE、AE的长以及扇形的半径AC,最后根据阴影部分面积=扇形ACF面积-△ACE面积-△CEF面积,进行计算即可.
解答  解:由旋转得,∠BCE=60°,BC=EC,AB=FE,
解:由旋转得,∠BCE=60°,BC=EC,AB=FE,
∴∠ECD=30°,
∵AB=CD=$\sqrt{3}$,
∴DE=1,CE=2=BC,
∴AE=AD-DE=2-1=1,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{7}$,
∴阴影部分面积
=扇形ACF面积-△ACE面积-△EFC面积
=$\frac{60×π×(\sqrt{7})^{2}}{360}$-$\frac{1}{2}$×1×$\sqrt{3}$-$\frac{1}{2}$×2×$\sqrt{3}$
=$\frac{7}{6}π$-$\frac{\sqrt{3}}{2}$-$\sqrt{3}$
=$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.
故答案为:$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$
点评 本题以旋转为背景,主要考查了矩形的性质和扇形的面积公式.求阴影面积常用的方法有:①直接用公式法; ②和差法; ③割补法.解题时注意:求阴影面积的主要思路是将不规则图形面积转化为规则图形面积的和差关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
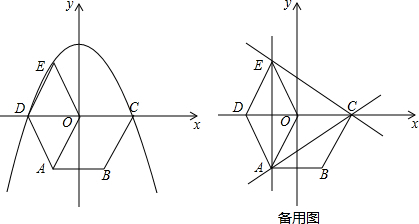
 如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.
如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
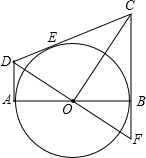 如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上).
如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
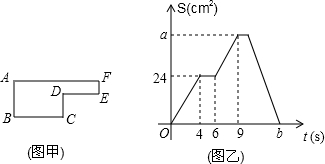
 购买一种水果,所付款金额(元)与购买数量(千克)之间的函数图象由线段OA和射线AB组成,如图所示,则一次购买20千克这种水果,比分两次每次购买10千克这种水果可以节省的费用为( )
购买一种水果,所付款金额(元)与购买数量(千克)之间的函数图象由线段OA和射线AB组成,如图所示,则一次购买20千克这种水果,比分两次每次购买10千克这种水果可以节省的费用为( )| A. | 20元 | B. | 12元 | C. | 10元 | D. | 8元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com