
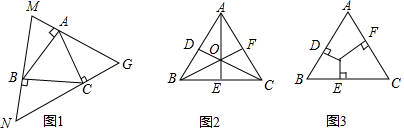
分析 (1)①本题中△ABC为等边三角形,AB=BC=a,∠ABC=60°,求出∠N=∠G=∠M=60°,即可得出结论;
②在直角△AMB、△CNB中,可以先求出BM和BN的长,即可得出结果;
(2)①由等边三角形的性质得出OD=OE=OF=$\frac{1}{2}$OB,AD=BE=CF=$\frac{1}{2}$AC=$\sqrt{3}$,OD+OE+OF=BF,由勾股定理求出BF即可;
②由等边三角形的面积得出第一个猜想成立;由勾股定理得出第二个猜想成立.
解答 (1)①证明:∵△ABC为等边三角形,
∴∠ABC=60°.AB=BC=AC,
∵BC⊥MN,BA⊥MG,
∴∠CBM=∠BAM=90°.
∴∠ABM=90°-∠ABC=30°.
∴∠M=90°-∠ABM=60°.
同理:∠N=∠G=60°.
∴△MNG为等边三角形.
②解:在Rt△ABM中,BM=$\frac{AB}{sinM}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4,
在Rt△BCN中,BN=$\frac{BC}{tanN}$=$\frac{2\sqrt{3}}{\sqrt{3}}$=2,
∴MN=BM+BN=6.
(2)解:①∵△ABC是等边三角形,点O是△ABC的三条高的交点,
∴OD=OE=OF=$\frac{1}{2}$OB,AD=BE=CF=$\frac{1}{2}$AC=$\sqrt{3}$,
∴OD+OE+OF=BF=$\sqrt{B{C}^{2}-C{F}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}$=3;
AD+BE+CF=3$\sqrt{3}$;
故答案为:3;3$\sqrt{3}$;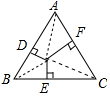
②①中的两个猜想仍然成立;理由如下:
连接OA、OB、OC,如图所示:
由①得:△ABC的面积=$\frac{1}{2}$×2$\sqrt{3}$×3=3$\sqrt{3}$,
又∵△ABC的面积=△OAB的面积+△OBC的面积+△OAC的面积=$\frac{1}{2}$AB•OD+$\frac{1}{2}$BC•OE+$\frac{1}{2}$AC•OF=$\frac{1}{2}$(OD+OE+OF)•AB=3$\sqrt{3}$,
∴OD+OE+OF=$\frac{2×3\sqrt{3}}{2\sqrt{3}}$=3;
设AB=BC=AC=a,根据勾股定理得:
BE2+OE2=OB2=BD2+OD2①,
CF2+OF2=OC2=CE2+OE2②,
AD2+OD2=AO2=AF2+OF2③,
①+②+③得:BE2+CF2+AD2=BD2+CE2+AF2,
∴BE2+CF2+AD2=(a-AD)2+(a-BE)2+(a-CF)2=a2-2AD•a+AD2+a2-2BE•a+BE2+a2-2CF•a+CF2
整理得:2a(AD+BE+CF)=3a2
∴AD+BE+CF=$\frac{3}{2}$a=$\frac{3}{2}$×2$\sqrt{3}$=3$\sqrt{3}$.
点评 本题是三角形综合题目,考查了等边三角形的性质与判定、三角函数、勾股定理以及三角形面积的计算等知识;本题综合性强,有一定难度,熟练掌握等边三角形的性质和勾股定理是解决问题的关键.


科目:初中数学 来源: 题型:解答题
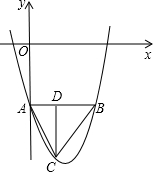 如图,已知二次函数y=ax2+bx+c的图象的顶点的坐标为(2,-9),与y轴交于点A(0,-5).
如图,已知二次函数y=ax2+bx+c的图象的顶点的坐标为(2,-9),与y轴交于点A(0,-5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
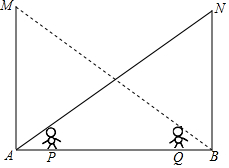 如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽.
如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ABC中,∠ACB=90°,分别以边AB、AC、BC为边分别向外作等边三角形,其面积分别为S1,S2,S3,若S1=6,S2=2,则S3=8.
如图,Rt△ABC中,∠ACB=90°,分别以边AB、AC、BC为边分别向外作等边三角形,其面积分别为S1,S2,S3,若S1=6,S2=2,则S3=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com