
”¾ĢāÄæ”æѧŠ£×¼±øŌŚø÷°ąÉčĮ¢Ķ¼Źé½ĒŅŌ·įø»Ķ¬Ń§ĆĒµÄæĪÓąĪÄ»ÆÉś»ī£®ĪŖĮĖøüŗĻĄķµÄ“īÅäø÷ĄąŹé¼®£¬Ń§Š£ĶÅĪÆŅŌ”°ĪŅ×īĻ²°®µÄŹé¼®”±ĪŖÖ÷Ģā£¬¶Ōѧɜ×īĻ²°®µÄŅ»ÖÖŹé¼®ĄąŠĶ½ųŠŠĖ껜³éŃłµ÷²é£¬ŹÕ¼ÆÕūĄķŹż¾Żŗ󣬻ęÖĘ³öŅŌĻĀĮ½·łĪ“Ķź³ÉµÄĶ³¼ĘĶ¼£¬Ēėøł¾ŻĶ¼¢ŁŗĶĶ¼¢ŚĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
 ””””””””
””””””””
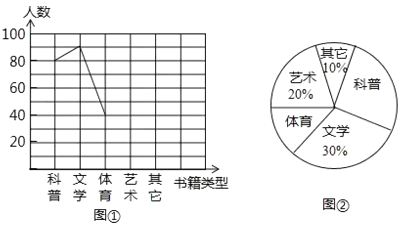
£Ø1£©ŌŚÕā“Ī³éŃłµ÷²éÖŠ£¬Ņ»¹²µ÷²éĮĖ_____________Ćūѧɜ£»
£Ø2£©Ēė°ŃÕŪĻßĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©ŌŚĶ³¼ĘĶ¼¢ŚÖŠ£¬Ēó³ö”°ĢåÓż”±²æ·ÖĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹż£»
£Ø4£©ČōøĆŠ£ÓŠŃ§Éś2400ČĖ£¬¹Ą¼ĘĻ²»¶”°æĘĘÕ”±Źé¼®µÄÓŠ¶ąÉŁČĖ£æ
”¾“š°ø”æ£Ø1£©300Ćū£»£Ø2£©“š°ø¼ū½āĪö£»£Ø3£©48”ć£»£Ø4£©640ČĖ£®
”¾½āĪö”æ
£Ø1£© ÓĆ×īĻ²°®ĪÄ×ÖĄąµÄČĖŹż³żŅŌ×īĻ²°®ĪÄ×ÖĄąµÄĖłÕ¼°Ł·Ö±Č¼“æÉĒó½āŅ»¹²µ÷²éµÄѧɜµÄ×ÜČĖŹż¼“Ńł±¾×ÜĮ棻
£Ø2£©ÓĆ×īĻ²°®ŅÕŹõĄąĖłÕ¼µÄ°Ł·Ö±Č³ĖŅŌ²ĪÓėµ÷²éµÄ×ÜČĖŹżĒó½ā×īĻ²°®ŅÕŹõĄąµÄ×ÜČĖŹż£¬ÓĆĘäĖüĖłÕ¼µÄ°Ł·Ö±Č³ĖŅŌµ÷²éČĖŹżµÄ×ÜČĖŹżĒó½āĘäĖüµÄČĖŹż£¬øł¾ŻĖłĒó²¹³äÕŪĻßĶ³¼ĘĶ¼¼“æÉ£»
£Ø3£©ÓĆ×īĻ²°®ĢåÓżĄąĖłÕ¼µÄ°Ł·Ö±Č³ĖŅŌ360”ć¼“æÉĒó³öĘäĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹż£»
£Ø4£©ÓÉŃł±¾¹Ą¼Ę×ÜĢåæÉµĆ£¬ÓĆ×īĻ²°®æĘĘÕĖłÕ¼µÄ°Ł·Ö±Č³ĖŅŌøĆ֊ѧµÄѧɜ×ÜŹż¼“æÉĒó½ā.
£Ø1£©£ŗÓɵŚŅ»øöÕŪĻßĶ¼æÉŅŌÖŖµĄ×īĻ²°®ĪÄ×ÖĄąµÄČĖŹżĪŖ90ČĖ£¬
“ÓµŚ¶žøöÉČŠĪĶ¼æÉŅŌÖŖµĄ×īĻ²°®ĪÄ×ÖĄąµÄĖłÕ¼°Ł·Ö±ČŹĒ30£„£¬
ĖłŅŌµ÷²é×ÜČĖŹż£ŗ![]() £ØĆū£©£¬
£ØĆū£©£¬
Ņņ“Ė£¬ŌŚÕā“Ī³éŃłµ÷²éÖŠ£¬Ņ»¹²µ÷²éĮĖ300Ćūѧɜ£»
£Ø2£©£ŗÓÉ£Ø1£©ÖŖµ÷²é×ÜČĖŹżŹĒ300£¬Ņņ“ĖæɵĆ:
Ļ²°®ŅÕŹõµÄÓŠ£ŗ![]() (Ćū)£¬
(Ćū)£¬
Ļ²°®ĘäĖüµÄÓŠ£ŗ![]() (Ćū)
(Ćū)
²¹Č«µÄÕŪĻßĶ³¼ĘĶ¼£¬ČēĻĀĶ¼ĖłŹ¾£ŗ

£Ø3£©£ŗĪŅĆĒÖŖµĄ£¬Ō²Ėł¶ŌÓ¦µÄŌ²ŠÄ½ĒŹĒ![]() £¬
£¬
“ÓĶ¼1ÖŖµĄ×īĻ²°®ĢåÓżµÄČĖŹżÓŠ40Ćū£¬µ÷²é×ÜČĖŹżŹĒ300Ćū£¬
Ņņ“Ė£¬”°ĢåÓż”±²æ·ÖĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹż£ŗ![]() £¬
£¬
“š£ŗŌŚĶ³¼ĘĶ¼¢ŚÖŠ£¬”°ĢåÓż”±²æ·ÖĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹżĪŖ![]() £®
£®
£Ø4£©£ŗ“ÓĶ¼1µÄÕŪĻßĶ¼ÖŖµĄ×īĻ²°®æĘĘÕµÄČĖŹżÓŠ80Ćū£¬µ÷²é×ÜČĖŹżµÄĪŖ300Ćū£¬
ĖłŅŌøĆŠ£Ļ²»¶”°æĘĘÕ”±Źé¼®µÄ“óŌ¼ÓŠ£ŗ![]() (ČĖ)
(ČĖ)
“š£ŗ¹Ą¼ĘøĆŠ£Ļ²»¶”°æĘĘÕ”±Źé¼®µÄ“óŌ¼ÓŠ640ČĖ.


 ÓĄĒ¬½ĢÓżŗ®¼Ł×÷ŅµæģĄÖ¼ŁĘŚŃÓ±ßČĖĆń³ö°ęÉēĻµĮŠ“š°ø
ÓĄĒ¬½ĢÓżŗ®¼Ł×÷ŅµæģĄÖ¼ŁĘŚŃÓ±ßČĖĆń³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=©2x2+8x©6ÓėxÖį½»ÓŚµćA”¢B£¬°ŃÅ×ĪļĻßŌŚxÖį¼°ĘäÉĻ·½µÄ²æ·Ö¼Ē×÷C1£¬½«C1ĻņÓŅĘ½ŅʵĆC2£¬C2ÓėxÖį½»ÓŚµćB£¬D£®ČōÖ±Ļßy=x+mÓėC1”¢C2¹²ÓŠ3øö²»Ķ¬µÄ½»µć£¬ŌņmµÄȔֵ·¶Ī§ŹĒ£Ø””””£©

A. ©2£¼m£¼![]() B. ©3£¼m£¼©
B. ©3£¼m£¼©![]() C. ©3£¼m£¼©2 D. ©3£¼m£¼©
C. ©3£¼m£¼©2 D. ©3£¼m£¼©![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬Ö±Ļß
ÖŠ£¬Ö±Ļß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬Óė
£¬Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() Å×ĪļĻß
Å×ĪļĻß![]() µÄ¶Ō³ĘÖįŹĒÖ±Ļß
µÄ¶Ō³ĘÖįŹĒÖ±Ļß![]() Óė
Óė![]() ÖįµÄ½»µćĪŖµć
ÖįµÄ½»µćĪŖµć![]() ĒŅ¾¹żµć
ĒŅ¾¹żµć![]() Į½µć£®
Į½µć£®
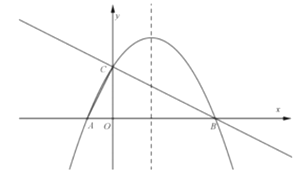
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µć![]() ĪŖÅ×ĪļĻ߶Ō³ĘÖįÉĻŅ»¶Æµć£¬µ±
ĪŖÅ×ĪļĻ߶Ō³ĘÖįÉĻŅ»¶Æµć£¬µ±![]() µÄÖµ×īŠ”Ź±£¬ĒėÄćĒó³öµć
µÄÖµ×īŠ”Ź±£¬ĒėÄćĒó³öµć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
£Ø3£©Å×ĪļĻßÉĻŹĒ·ń“ęŌŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÖįÓŚµć
ÖįÓŚµć![]() Ź¹µĆŅŌµć
Ź¹µĆŅŌµć![]() ĪŖ¶„µćµÄČż½ĒŠĪÓė
ĪŖ¶„µćµÄČż½ĒŠĪÓė![]() ĻąĖĘ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµć
ĻąĖĘ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻÉĢŅŹĒĖģÄžŹŠÄ³µŲµÄĢŲÉ«Ź±ĮīĖ®¹ū£®ĻÉĢŅŅ»ÉĻŹŠ£¬Ė®¹ūµźµÄĄĻ°åÓĆ2400ŌŖ¹ŗ½ųŅ»ÅśĻÉĢŅ£¬ŗÜæģŹŪĶź£»ĄĻ°åÓÖÓĆ3700ŌŖ¹ŗ½ųµŚ¶žÅśĻÉĢŅ£¬Ėł¹ŗ¼žŹżŹĒµŚŅ»ÅśµÄ![]() ±¶£¬µ«½ų¼Ū±ČµŚŅ»ÅśĆ漞¶ąĮĖ5ŌŖ£®
±¶£¬µ«½ų¼Ū±ČµŚŅ»ÅśĆ漞¶ąĮĖ5ŌŖ£®
£Ø1£©µŚŅ»ÅśĻÉĢŅĆ漞½ų¼ŪŹĒ¶ąÉŁŌŖ£æ
£Ø2£©ĄĻ°åŅŌĆ漞225ŌŖµÄ¼ŪøńĻśŹŪµŚ¶žÅśĻÉĢŅ£¬ŹŪ³ö80%ŗó£¬ĪŖĮĖ¾”æģŹŪĶź£¬Ź£ĻĀµÄ¾ö¶Ø“ņÕŪ“ŁĻś£®ŅŖŹ¹µĆµŚ¶žÅśĻÉĢŅµÄĻśŹŪĄūČó²»ÉŁÓŚ440ŌŖ£¬Ź£ÓąµÄĻÉĢŅĆ漞ŹŪ¼ŪÖĮÉŁ“ņ¼øÕŪ£æ£ØĄūČó£½ŹŪ¼Ū©½ų¼Ū£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”收Ėļ×ÓĖć¾”·ŹĒÖŠ¹ś“«Ķ³ŹżŃ§×īÖŲŅŖµÄÖų×÷,Ō¼³ÉŹéÓŚĖÄ”¢ĪåŹĄ¼Ķ.ĻÖŌŚ“«±¾µÄ”¶Ėļ×ÓĖć¾”·¹²Čż¾ķ.¾ķÉĻŠšŹöĖć³ļ¼ĒŹżµÄׯŗįĻą¼äÖʶČŗĶ³ļĖć³Ė³ż·ØŌņ;¾ķÖŠ¾ŁĄżĖµĆ÷³ļĖć·ÖŹżĖć·ØŗĶ³ļĖćæŖĘ½·½·Ø;¾ķĻĀ¼ĒĀ¼ĖćĢā,²»µ«Ģį¹©ĮĖ“š°ø,¶ųĒŅ»¹øų³öĮĖ½ā·Ø.ĘäÖŠ¼ĒŌŲ:”°½ńӊľ,²»ÖŖ³¤¶Ģ.ŅżÉž¶ČÖ®,ӹɞĖijßĪå,ĒüÉžĮæÖ®,²»×ćŅ»³ß.ĪŹÄ¾³¤¼øŗĪ?”±
ŅėĪÄ:”°ÓĆŅ»øłÉž×ÓČ„ĮæŅ»øł³¤Ä¾,Éž×Ó»¹Ź£Óą4.5³ß,½«Éž×Ó¶ŌÕŪŌŁĮ泤ľ,³¤Ä¾»¹Ź£Óą1³ß,ĪŹ³¤Ä¾³¤¶ąÉŁ³ß?”±
Ēė½ā“šÉĻŹöĪŹĢā.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
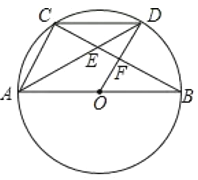
”¾ĢāÄæ”æČēĶ¼£¬![]() ĪŖ
ĪŖ![]() µÄÖ±¾¶£¬
µÄÖ±¾¶£¬![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬
µÄÖŠµć£¬![]() Óė
Óė![]() ·Ö±š½»ÓŚµć
·Ö±š½»ÓŚµć![]() £®
£®
£Ø1£©ĒóÖ¤£ŗ![]() £®
£®
£Ø2£©ĒóÖ¤£ŗ![]() £»
£»
£Ø3£©Čō![]() µÄÖ±¾¶
µÄÖ±¾¶![]() £¬Ēó
£¬Ēó![]() µÄ³¤£®
µÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
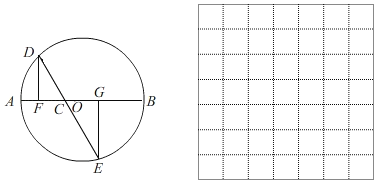
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬AB=4cm£¬CĪŖABÉĻŅ»¶Æµć£¬¹żµćCµÄÖ±Ļß½»”ŃOÓŚD”¢EĮ½µć£¬ĒŅ”ĻACD=60”ć£¬DF”ĶABÓŚµćF£¬EG”ĶABÓŚµćG£¬µ±µćCŌŚABÉĻŌĖ¶ÆŹ±£¬ÉčAF=xcm£¬DE=ycm(µ±xµÄÖµĪŖ0»ņ3Ź±£¬yµÄÖµĪŖ2)£¬Ģ½¾æŗÆŹżyĖę×Ō±äĮæxµÄ±ä»Æ¶ų±ä»ÆµÄ¹ęĀÉ£®
£Ø1£©ĶعżČ”µć”¢»Ķ¼”¢²āĮ棬µĆµ½ĮĖxÓėyµÄ¼ø×é¶ŌÓ¦Öµ£¬ČēĻĀ±ķ£ŗ
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
£Ø2£©½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ£¬Ćč³öŅŌ²¹Č«ŗóµÄ±ķÖŠø÷¶Ō¶ŌÓ¦ÖµĪŖ×ų±źµÄµć£¬»³öøĆŗÆŹżµÄĶ¼Ļó£»
£Ø3£©½įŗĻ»³öµÄŗÆŹżĶ¼Ļ󣬽ā¾öĪŹĢā£ŗµćFÓėµćOÖŲŗĻŹ±£¬DE³¤¶ČŌ¼ĪŖ””””””””cm(½į¹ū±£ĮōŅ»Ī»Š”Źż)£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
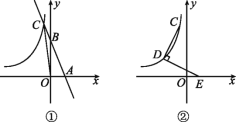
”¾ĢāÄæ”æČēĶ¼¢Ł£¬Ö±Ļßy=-2x+4½»xÖį”¢yÖįÓŚA£¬BĮ½µć£¬½»Ė«ĒśĻßy=![]() (x<0)ÓŚCµć£¬”÷OACµÄĆ껿ĪŖ6£®
(x<0)ÓŚCµć£¬”÷OACµÄĆ껿ĪŖ6£®
(1)ĒóĖ«ĒśĻߵĽāĪöŹ½£»
(2)ČēĶ¼¢Ś£¬DĪŖĖ«ĒśĻßy=![]() (x<0)ÉĻŅ»µć£¬Į¬½ÓCD£¬½«Ļ߶ĪCDČʵćDĖ³Ź±ÕėŠż×Ŗ90”ćµĆĻ߶ĪDE£¬µćEĒ”ŗĆĀäŌŚxÖįÉĻ£¬ĒóµćEµÄ×ų±ź£®
(x<0)ÉĻŅ»µć£¬Į¬½ÓCD£¬½«Ļ߶ĪCDČʵćDĖ³Ź±ÕėŠż×Ŗ90”ćµĆĻ߶ĪDE£¬µćEĒ”ŗĆĀäŌŚxÖįÉĻ£¬ĒóµćEµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖæŖæŚĻņÉĻµÄÅ×ĪļĻß![]() ½»
½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬
£¬![]() £¬ŗÆŹżÖµ
£¬ŗÆŹżÖµ![]() µÄ×īŠ”ÖµŹĒ
µÄ×īŠ”ÖµŹĒ![]() £®
£®
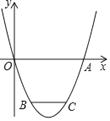
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£®
£Ø2£©µć![]() ĪŖÅ×ĪļĻßÉĻµÄµć£¬²¢ŌŚ¶Ō³ĘÖįµÄ×ó²ą£®×÷
ĪŖÅ×ĪļĻßÉĻµÄµć£¬²¢ŌŚ¶Ō³ĘÖįµÄ×ó²ą£®×÷![]() Öį½»Å×ĪļĻßÓŚµć
Öį½»Å×ĪļĻßÓŚµć![]() £¬Į¬½į
£¬Į¬½į![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() £®
£®
¢ŁĒó![]() µÄÖµ£®
µÄÖµ£®
¢ŚČōµć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻ£¬ŅŌµć
ÉĻ£¬ŅŌµć![]() ĪŖŌ²ŠÄ£¬
ĪŖŌ²ŠÄ£¬![]() ĪŖ°ė¾¶»Ō²£®µ±
ĪŖ°ė¾¶»Ō²£®µ±![]() ŗĶ
ŗĶ![]() µÄŅ»±ßĻąĒŠŹ±£¬Ēóµć
µÄŅ»±ßĻąĒŠŹ±£¬Ēóµć![]() µÄŗį×ų±ź£®
µÄŗį×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com