
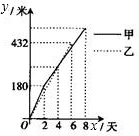
 程队所挖隧道的长度y(米)与挖掘时间x(天)之间的函数图象.请根据图象所提供的信息解答下列问题:
程队所挖隧道的长度y(米)与挖掘时间x(天)之间的函数图象.请根据图象所提供的信息解答下列问题: 解:(1)设y乙=kx(0≤x≤6),y甲=mx+n(2≤x≤8),
解:(1)设y乙=kx(0≤x≤6),y甲=mx+n(2≤x≤8), ,
,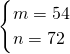 ,即y甲=54x+72(1分)
,即y甲=54x+72(1分)

科目:初中数学 来源: 题型:
| 1 |
| 100 |
| 99 |
| 100 |
| 294 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
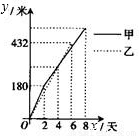
 程队所挖隧道的长度y(米)与挖掘时间x(天)之间的函数图象.请根据图象所提供的信息解答下列问题:
程队所挖隧道的长度y(米)与挖掘时间x(天)之间的函数图象.请根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源:2013年5月中考数学模拟试卷(10)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2012年河北省中考数学模拟试卷(十七)(解析版) 题型:解答题
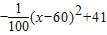 (万元),当地政府拟在“十二五”规划中加快开发该特产的销售,其规划方案为:规划后对该项目每年投入100万元,在实施规划的5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每年投入x万元,可获利润
(万元),当地政府拟在“十二五”规划中加快开发该特产的销售,其规划方案为:规划后对该项目每年投入100万元,在实施规划的5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每年投入x万元,可获利润 (万元)
(万元)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com