
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A. 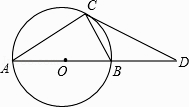
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
【答案】
(1)证明:如图,连接OC.
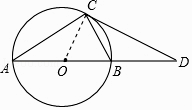
∵AB是⊙O的直径,C是⊙O上一点,
∴∠ACB=90°,即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,
∴∠ACO=∠A=∠BCD,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴CD是⊙O的切线.
(2)解:在Rt△OCD中,∠OCD=90°,OC=3,CD=4,
∴OD= ![]() =5,
=5,
∴BD=OD﹣OB=5﹣3=2.
【解析】(1)连接OC,由AB是⊙O的直径可得出∠ACB=90°,即∠ACO+∠OCB=90°,由等腰三角形的性质结合∠BCD=∠A,即可得出∠OCD=90°,即CD是⊙O的切线;(2)在Rt△OCD中,由勾股定理可求出OD的值,进而可得出BD的长.


科目:初中数学 来源: 题型:
【题目】某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.
(1)求每个甲种配件、每个乙种配件的价格分别为多少万元;
(2)现投入资金80万元,根据维修需要预测,甲种配件要比乙种配件至少要多22件,问乙种配件最多可购买多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=![]() ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市南县大力发展农村旅游事业,全力打造“洞庭之心湿地公园”,其中罗文村的“花海、涂鸦、美食”特色游享誉三湘,游人如织.去年村民罗南洲抓住机遇,返乡创业,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮利润是住宿利润的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的利润各为多少万元?
(2)今年罗南洲把去年的餐饮利润全部用于继续投资,增设了土特产的实体店销售和网上销售项目.他在接受记者采访时说:“我预计今年餐饮和住宿的利润比去年会有10%的增长,加上土特产销售的利润,到年底除收回所有投资外,还将获得不少于10万元的纯利润.”请问今年土特产销售至少有多少万元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
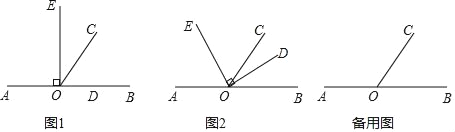
【题目】如图所示,在直线AB上的一点O,以O为端点依次作射线OE,OC,OD,使∠EOD=90°,∠COB=60°
(1)如图1当∠EOD的一边OD在射线OB上时,求∠COE的度数;
(2)如图2当∠EOD绕着点O逆时针旋转到OC平分∠BOE时,求∠COD的度数;
(3)当∠EOD绕着点O逆时针旋转,且O°<∠AOE<90°(但≠60°)时,试猜想∠AOE与∠COD有怎样的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A.众数是8
B.中位数是3
C.平均数是3
D.方差是0.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.
(1)求点C的坐标;
(2)当△MCN的周长与四边形OMNB的周长相等时,求CM的长;
(3)在OB上是否存在点Q,使得△MNQ为等腰直角三角形?若存在,请求出此时MN的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( ) 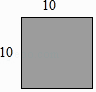
A.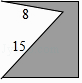
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com