
 如图,四边形ABCD的面积为1,顺次连结ABCD各边中点得到四边形A1B1C1D1,再顺次连结各边中点得到四边形A2B2C2D2;重复同样的方法直到得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.
如图,四边形ABCD的面积为1,顺次连结ABCD各边中点得到四边形A1B1C1D1,再顺次连结各边中点得到四边形A2B2C2D2;重复同样的方法直到得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$. 分析 连接对角线,运用三角形中位线定理可得$\frac{B{A}_{1}}{BA}$=$\frac{B{B}_{1}}{BC}$=$\frac{{A}_{1}{B}_{1}}{AC}$=$\frac{1}{2}$,根据相似三角形的性质可得S△BB1AI=$\frac{1}{4}$S△BCA,同理可得S△DD1C1=$\frac{1}{4}$S△DAC,即S△BB1AI+S△DD1C1=$\frac{1}{4}$(S△DAC+S△BCA)=$\frac{1}{4}$S四边形ABCD,进而可得答案.
解答 解:连接AC,BD.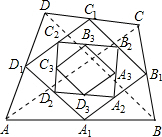
∵四边形A1B1C1D1是顺次连接各中点得到的,
∴$\frac{B{A}_{1}}{BA}$=$\frac{B{B}_{1}}{BC}$=$\frac{{A}_{1}{B}_{1}}{AC}$=$\frac{1}{2}$,
故△BB1AI∽△BCA,相似比为$\frac{1}{2}$,面积比为$\frac{1}{4}$,即S△BB1AI=$\frac{1}{4}$S△BCA,
同理可得S△DD1C1=$\frac{1}{4}$S△DAC,即S△BB1AI+S△DD1C1=$\frac{1}{4}$(S△DAC+S△BCA)=$\frac{1}{4}$S四边形ABCD,
同理可得S△CC1B1+S△AA1D1=$\frac{1}{4}$S四边形ABCD,故
S△BB1AI+S△DD1C1+S△CC1B1+S△AA1D1=$\frac{1}{2}$S四边形ABCD,
则S四边形A1B1C1D1=$\frac{1}{2}$S四边形ABCD=$\frac{1}{2}$,
同理可得第二个小四边形的面积为$\frac{1}{2}$×$\frac{1}{2}$即$\frac{1}{{2}^{2}}$.
第三个面积为$\frac{1}{{2}^{3}}$,以此类推第n个四边形的面积为$\frac{1}{{2}^{n}}$.
故答案为:$\frac{1}{{2}^{n}}$.
点评 此题主要考查了中点四边形,解答此题的关键是求出四边形A1B1C1D1的面积,再依此类推求出第二,第三个四边形的面积,找出规律,即可求得第n个四边形的面积.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
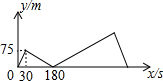 A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.
A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
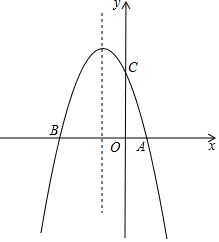 如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)
如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 检测一批灯泡的使用寿命 | |
| B. | 调查昆明《都市条形码》栏目的收视率 | |
| C. | 了解我省中学生视力情况 | |
| D. | 了解九(1)班学生校服的尺码情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
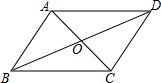 如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )
如图,?ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线的和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
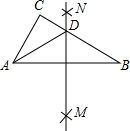 如图,在△ABC中,分别以点A和点B为圆心,以大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,若△ADC的周长为10,AB=6,则△ABC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,以大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,若△ADC的周长为10,AB=6,则△ABC的周长为( )| A. | 6 | B. | 12 | C. | 16 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com