
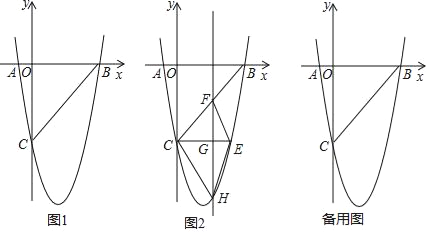
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨“—÷™Ň◊őÔŌŖy=ax2+bx©Ā5”Žx÷ŠĹĽ”ŕA£®©Ā1£¨0£©£¨B£®5£¨0£©ŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£ģ
£®1£©«ůŇ◊őÔŌŖĶńļĮ żĪŪīÔ Ĺ£Ľ
£®2£©»ÁÕľ2£¨CE°őx÷Š”ŽŇ◊őÔŌŖŌŗĹĽ”ŕĶ„E£¨Ķ„H «÷ĪŌŖCEŌ¬∑ĹŇ◊őÔŌŖ…ŌĶń∂ĮĶ„£¨ĻżĶ„H«“”Žy÷Š∆Ĺ––Ķń÷ĪŌŖ”ŽBC£¨CE∑÷ĪūŌŗĹĽ”ŕĶ„F£¨G£¨ ‘ŐĹĺŅĶĪĶ„H‘ň∂ĮĶĹļőī¶ Ī£¨ňńĪŖ–őCHEFĶń√śĽż◊Óīů£¨«ůĶ„HĶń◊ÝĪÍ£Ľ
£®3£©»ŰĶ„Kő™Ň◊őÔŌŖĶń∂•Ķ„£¨Ķ„M£®4£¨m£© «ł√Ň◊őÔŌŖ…ŌĶń“ĽĶ„£¨‘ŕx÷Š£¨y÷Š…Ō∑÷Īū’“Ķ„P£¨Q£¨ ĻňńĪŖ–őPQKMĶń÷‹≥§◊Ó–°£¨«ů≥ŲĶ„P£¨QĶń◊ÝĪÍ£ģ
°ĺīūįł°Ņ£®1£©y=x2©Ā4x©Ā5£®2£©£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ£®3£©P£®
£©£Ľ£®3£©P£®![]() £¨0£©£¨Q£®0£¨©Ā
£¨0£©£¨Q£®0£¨©Ā![]() £©
£©
°ĺĹ‚őŲ°Ņ’ŻŐŚ∑÷őŲ£ļ
£®1£©”√īż∂®ŌĶ ż∑®«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ£®2£©…ŤH(t£¨t2-4t-5)£¨”√ļ¨tĶńīķ ż ĹĪŪ ĺFHĶń≥§£¨«ů≥ŲCEĶń≥§£¨”√∂‘Ĺ«ŌŖĽ•ŌŗīĻ÷ĪĶńňńĪŖ–őĶń√śĽżĶ»”ŕ∂‘Ĺ«ŌŖĽżĶń“ĽįŽ£¨į—ňńĪŖ–őCHEFĶń√śĽżĪŪ ĺő™Ļō”ŕtĶń∂ĢīőļĮ ż£¨”√∂ĢīőļĮ żĶń–‘÷ «ůĹ‚£Ľ£®3£©◊ųĶ„M£¨KĻō”ŕx÷Š£¨y÷Š∂‘≥∆Ķ„M°š£¨K°š£¨Ń¨Ĺ”M°šK°š£¨∑÷ĪūĹĽx÷Š£¨y÷Š”ŕĶ„P£¨Q£¨«ů≥ŲM°šK°šĶńĹ‚őŲ Ĺ£¨ľīŅ…Ķ√ĶĹĶ„P£¨QĶń◊ÝĪÍ.
Ĺ‚£ļ£®1£©į—A(-1£¨0)£¨B(5£¨0)īķ»Žy=ax2+bx-5Ķ√
![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]()
°ŗ∂ĢīőļĮ żĶńĪŪīÔ Ĺő™y=x2-4x-5
£®2£©»ÁÕľ2£¨…ŤH(t£¨t2-4t-5)£¨
°ŖCE||x÷Š£¨°ŗ-5=x2-4x-5£¨Ĺ‚Ķ√£¨x1=0£¨x2=4£¨
°ŗE(4£¨-5)£¨°ŗCE=4£¨
°ŖB(5£¨0)£¨C(0£¨-5)£¨
![]() °ŗ
°ŗ![]() £¨
£¨
°ŗ÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y2=x-5£¨°ŗF(t£¨t-5)£¨
°ŖCE||x÷Š£¨HF||y÷Š£¨°ŗCE°ÕHF£¨
°ŗňńĪŖ–őCHEFĶń√śĽż=![]() )2+
)2+![]() £¨
£¨
°ŗH(![]() .
.
£®3£©»ÁÕľ3£¨
°ŖĶ„Kő™∂•Ķ„£¨°ŗK(2£¨-9)£¨
°ŗĶ„KĻō”ŕy÷ŠĶń∂‘≥∆Ķ„K°šĶń◊ÝĪÍő™(-2£¨-9)£ģ
°ŖM(4£¨m)£¨°ŗM(4£¨-5)£¨
°ŗĶ„MĻō”ŕx÷ŠĶń∂‘≥∆Ķ„M°šĶń◊ÝĪÍő™(4£¨5)£ģ
…Ť÷ĪŌŖK°šM°šĶńĹ‚őŲ Ĺő™y3=a3x+b3£¨
![]() £¨°ŗ
£¨°ŗ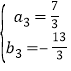
°ŗ÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y3=![]() £¨
£¨
°ŗP£¨QĶń◊ÝĪÍ∑÷Īūő™P(![]() £¨0)£¨Q(0£¨-
£¨0)£¨Q(0£¨-![]() .
.


 ”ŇĶ»…ķŐ‚Ņ‚ŌĶŃ–īūįł
”ŇĶ»…ķŐ‚Ņ‚ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
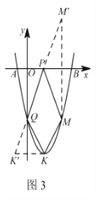
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™°ųABC÷–£¨°ŌB=90°„£¨AB=8cm£¨BC=6cm£¨P°ĘQ «°ųABCĪŖ…ŌĶńŃĹłŲ∂ĮĶ„£¨∆š÷–Ķ„Pī”Ķ„AŅ™ ľ—ōA°ķB∑ĹŌÚ‘ň∂Į£¨«“ňŔ∂»ő™√Ņ√Ž1cm£¨Ķ„Qī”Ķ„BŅ™ ľ—ōB°ķC°ķA∑ĹŌÚ‘ň∂Į£¨«“ňŔ∂»ő™√Ņ√Ž2cm£¨ňŁ√«Õ¨ Ī≥Ų∑Ę£¨…Ť≥Ų∑ĘĶń Īľšő™t√Ž£ģ
(1)≥Ų∑Ę2√Žļů£¨«ůPQĶń≥§£Ľ
(2)ĶĪĶ„Q‘ŕĪŖBC…Ō‘ň∂Į Ī£¨≥Ų∑Ęľł√Ž÷”£¨°ųPQBń‹–ő≥…Ķ»—Ł»żĹ«–ő£Ņ
(3)ĶĪĶ„Q‘ŕĪŖCA…Ō‘ň∂Į Ī£¨«ůń‹ Ļ°ųBCQ≥…ő™Ķ»—Ł»żĹ«–őĶń‘ň∂Į Īľš£Ľ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
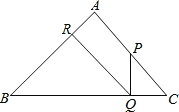
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™£ļ‘ŕ°ųABC÷–£¨°ŌA=90°„£¨AB=AC=1£¨P «AC…Ō≤Ľ”ŽA°ĘC÷ōļŌĶń“Ľ∂ĮĶ„£¨PQ°ÕBC”ŕQ£¨QR°ÕAB”ŕR£ģ
£®1£©«ů÷§£ļPQ=CQ£Ľ
£®2£©…ŤCPĶń≥§ő™x£¨QRĶń≥§ő™y£¨«ůy”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺľį◊‘ĪšŃŅxĶń»°÷Ķ∑∂őߣ¨≤Ę‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ◊ų≥ŲļĮ żÕľŌů£ģ
£®3£©PRń‹∑Ů∆Ĺ––”ŕBC£Ņ»ÁĻŻń‹£¨ ‘«ů≥ŲxĶń÷Ķ£Ľ»Ű≤Ľń‹£¨«ŽľÚ ŲņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ“ĽŐű ż÷Š…Ōī”◊ůĶĹ”““ņīő»°A£¨B£¨C»żłŲĶ„£¨«“ ĻĶ√Ķ„A£¨BĶĹ‘≠Ķ„OĶńĺŗņŽĺýő™1łŲĶ•őĽ≥§∂»£¨Ķ„CĶĹĶ„AĶńĺŗņŽő™7łŲĶ•őĽ≥§∂».
£®1£©‘ŕ ż÷Š…ŌĶ„AňýĪŪ ĺĶń ż «__________£¨Ķ„CňýĪŪ ĺĶń ż «_____________.
£®2£©»ŰĶ„P°ĘQ∑÷Īūī”Ķ„A°ĘCī¶≥Ų∑Ę£¨—ō ż÷Š“‘√Ņ√Ž1łŲĶ•őĽ≥§∂»ļÕ√Ņ√Ž3łŲĶ•őĽ≥§∂»ĶńňŔ∂»Õ¨ ĪŌÚ◊ů‘ň∂Į£¨‘ň∂Į Īľšő™t√Ž£¨ĶĪP°ĘQŃĹĶ„Ōŗĺŗő™4łŲĶ•őĽ≥§∂» Ī£¨«ůtĶń÷Ķ.

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨÷ĪĹ«◊ÝĪÍŌĶxOy÷–£¨“ĽīőļĮ ży=kx+bĶńÕľŌůl1∑÷Īū”Žx÷Š£¨y÷ŠĹĽ”ŕA£®15£¨0£©£¨BŃĹĶ„£¨’żĪ»ņżļĮ ży=![]() xĶńÕľŌůl2”Žl1ĹĽ”ŕĶ„C£®m£¨3£©£ģ
xĶńÕľŌůl2”Žl1ĹĽ”ŕĶ„C£®m£¨3£©£ģ
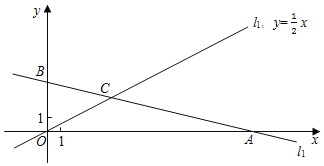
£®1£©«ůmĶń÷Ķľįl1ňý∂‘”¶Ķń“ĽīőļĮ żĪŪīÔ Ĺ£Ľ
£®2£©łýĺ›ÕľŌů£¨«Ž÷ĪĹ”–ī≥Ų‘ŕĶŕ“ĽŌůŌřńŕ£¨ĶĪ“ĽīőļĮ ży=kx+bĶń÷Ķīů”ŕ’żĪ»ņżļĮ ży=![]() xĶń÷Ķ Ī£¨◊‘ĪšŃŅxĶń»°÷Ķ∑∂őߣģ
xĶń÷Ķ Ī£¨◊‘ĪšŃŅxĶń»°÷Ķ∑∂őߣģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ£®1£©ĻŘ≤žňľŅľ£ļ»ÁÕľ£¨ŌŖ∂őAB…Ō”–ŃĹłŲĶ„C°ĘD£¨«Ž∑÷Īū–ī≥Ų“‘Ķ„A°ĘB°ĘC°ĘDő™∂ňĶ„ĶńŌŖ∂ő£¨≤Ęľ∆ň„Õľ÷–Ļ≤”–∂ŗ…ŔŐűŌŖ∂ő£Ľ
£®2£©ń£–ÕĻĻĹ®£ļ»ÁĻŻŌŖ∂ő…Ō”–młŲĶ„£®įŁņ®ŌŖ∂őĶńŃĹłŲ∂ňĶ„£©£¨‘Úł√ŌŖ∂ő…ŌĻ≤”–∂ŗ…ŔŐűŌŖ∂ő£Ņ«ŽňĶ√ųń„ĹŠ¬ŘĶń’ż»∑–‘£Ľ
£®3£©Õō’Ļ”¶”√£ļń≥įŗ45√ŻÕ¨—ß‘ŕĪŌ“ĶļůĶń“ĽīőĺŘĽŠ÷–£¨»Ű√ŅŃĹ»ňő’1īő ÷ő ļ√£¨ń«√īĻ≤ő’∂ŗ…Ŕīő ÷£Ņ
«ŽĹę’‚łŲő Ő‚◊™ĽĮő™…Ō Ųń£–Õ£¨≤Ę÷ĪĹ””¶”√…Ō Ųń£–ÕĶńĹŠ¬ŘĹ‚ĺŲő Ő‚£ģ
![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ķ„A°ĘB◊ÝĪÍ∑÷Īūő™£®4£¨0£©°Ę£®0£¨8£©£¨Ķ„C «ŌŖ∂őOB…Ō“Ľ∂ĮĶ„£¨Ķ„E‘ŕx÷Š’żįŽ÷Š…Ō£¨ňńĪŖ–őOEDC «ĺō–ő£¨«“OE=2OC£ģ…ŤOE=t(t>0)£¨ĺō–őOEDC”Ž°ųAOB÷ōļŌ≤Ņ∑÷Ķń√śĽżő™S£ģłýĺ›…Ō ŲŐűľĢ£¨ĽōīūŌ¬Ń–ő Ő‚£ļ
£®1£©ĶĪĺō–őOEDCĶń∂•Ķ„D‘ŕ÷ĪŌŖAB…Ō Ī£¨t= £Ľ
£®2£©ĶĪt=4 Ī£¨÷ĪĹ”–ī≥ŲSĶń÷Ķ£Ľ
£®3£©«ů≥ŲS”ŽtĶńļĮ żĻōŌĶ Ĺ£Ľ
£®4£©»ŰS=12£¨‘Út= £ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
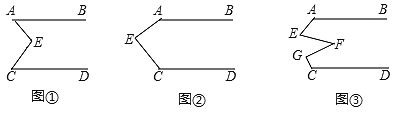
°ĺŐ‚ńŅ°Ņ£®ł–÷™£©»ÁÕľĘŔ£¨AB°őCD£¨Ķ„E‘ŕ÷ĪŌŖAB”ŽCD÷ģľš£¨Ń¨ĹŠAE°ĘBE£¨ ‘ňĶ√ų°ŌBAE+°ŌDCE=°ŌAEC£Ľ
£®ŐĹĺŅ£©ĶĪĶ„E‘ŕ»ÁÕľĘŕĶńőĽ÷√ Ī£¨∆šňŻŐűľĢ≤ĽĪš£¨ ‘ňĶ√ų°ŌAEC+°ŌBAE+°ŌDCE=360°„£Ľ
£®”¶”√£©Ķ„E°ĘF°ĘG‘ŕ÷ĪŌŖAB”ŽCD÷ģľš£¨Ń¨ĹŠAE°ĘEF°ĘFGļÕCG£¨∆šňŻŐűľĢ≤ĽĪš£¨»ÁÕľĘŘ£¨»Ű°ŌEFG=36°„£¨‘Ú°ŌBAE+°ŌAEF+°ŌFGC+°ŌDCG=______°„.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅĻ≤ŌŪĶ•≥ĶĪĽ”Ģő™°į–¬ňńīů∑Ę√ų°Ī÷ģ“Ľ£¨»ÁÕľ1ňý ĺ «ń≥Ļęňĺ2017ńÍŌÚ–Ň—Ű –≥°ŐŠĻ©“Ľ÷÷Ļ≤ŌŪ◊‘––≥ĶĶń ĶőÔÕľ£¨≥Ķľ‹ĶĶAC”ŽCDĶń≥§∑÷Īūő™45cm£¨60cm£¨AC°ÕCD£¨◊ýłňCEĶń≥§ő™20cm£¨Ķ„A£¨C£¨E‘ŕÕ¨“ĽŐű÷ĪŌŖ…Ō£¨«“°ŌCAB=75°„£¨»ÁÕľ2£ģ
£®1£©«ů≥Ķľ‹ĶĶADĶń≥§£Ľ
£®2£©«ů≥Ķ◊ýĶ„EĶĹ≥Ķľ‹ĶĶABĶńĺŗņŽ£ģ£®ĹŠĻŻĺę»∑ĶĹ1cm£¨≤őŅľ żĺ›£ļsin75°„=0.9659£¨cos75°„=0.2588£¨tan75°„=3.7321£©

≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com