
【题目】二次函数![]() (
(![]() ,
,![]() 为常数,
为常数,![]() )的图象记为L.
)的图象记为L.
(1)若![]() =1,
=1,![]() =3,求图象L的顶点坐标;
=3,求图象L的顶点坐标;
(2)若图象L过点(4,1),且2≤a≤5,求![]() 的最大值;
的最大值;
(3)若![]() ,点
,点![]() ,
,![]() 在图象L上,当
在图象L上,当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
____________ |
|
|
方程有两个不相等的正实根 | ____________ | ____________ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息技术飞速发展的今天,智能手机的使用呈现出低龄化的趋势,中小学生使用智能手机成为十分普遍的现象,但智能手机给生活带来便利的同时,也对中小学生的身心发展带来一些不利影响,比如手机屏幕对视力的伤害、关注各种“垃圾新闻”对时间的浪费、沉迷手机游戏缺少运动、人际交往等等,这些现象引起了家长、学校、社会的广泛关注.对此,成都某中学学生会发出了“中小学生使用非智能手机”的倡议,鼓励同学们全面发展,追逐梦想,把更多时间用在将来能够成就自我的地方.据统计,今年9月该中学使用非智能手机的同学有128人,倡议发出后,11月使用非智能手机的同学上升到了200人.
(1)若从9月到11月使用非智能手机的同学平均增长率相同,那么按此增长率增长到12月份该校使用非智能手机的同学将有多少人?
(2)某于机制造商发现当下市场上售卖的非智能手机大多品质不佳、外观设计成就,难以满足市场的需要,所以该厂决定投入12万元全部用于生产![]() 型、
型、![]() 型两款精美的“学生专用手机”投入市场,一部
型两款精美的“学生专用手机”投入市场,一部![]() 型手机生产成本为400元,售价为600元;一部
型手机生产成本为400元,售价为600元;一部![]() 型手机生产成本为600元,售价为930元,该厂计划生产
型手机生产成本为600元,售价为930元,该厂计划生产![]() 型手机的数量不少于
型手机的数量不少于![]() 型手机数量的2倍,但不超过
型手机数量的2倍,但不超过![]() 型手机数量的2.3倍,求生产这批手机并全部售卖后可获得的最大利润.
型手机数量的2.3倍,求生产这批手机并全部售卖后可获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.

现商家设计了2种棱柱体包装盒,其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率=![]() ×100%)
×100%)

(1)请分别计算出图2与图3中的底面利用率(结果保留到0.1%);
(2)考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于点A、B,且过点C(4,3).
轴相交于点A、B,且过点C(4,3).
(1)求![]() 的值和该抛物线顶点P的坐标;
的值和该抛物线顶点P的坐标;
(2)将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的对角线相交于O,点P在射线AO上,∠MPN=90°.
(1)如图1,当P与点O重合,M、N分别在AD、AB上,AM=2DM,则![]() =__________;
=__________;
(2)如图2,点P在CO上,AP=2CP,M为AD的中点,求![]() 的值.
的值.
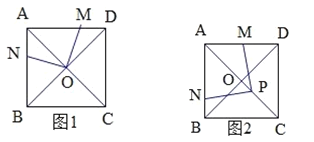
(3)如图3,P在AC的延长线上,M为AD的中点,AP=nCP,则![]() =____________(用含n的式子表示)
=____________(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
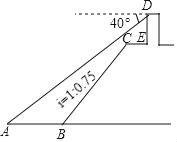
【题目】如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
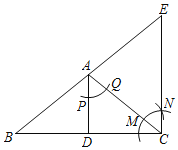
【题目】如图,在△ABC中,AD为边BC上的中线,且AD平分∠BAC.嘉淇同学先是以A为圆心,任意长为半径画弧,交AD于点P,交AC于点Q,然后以点C为圆心,AP长为半径画弧,交AC于点M,再以M为圆心,PQ长为半径画弧,交前弧于点N,作射线CN,交BA的延长线于点E.
(1)通过嘉淇的作图方法判断AD与CE的位置关系是 ,数量关系是 ;
(2)求证:AB=AC;
(3)若BC=24,CE=10,求△ABC的内心到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线过O、A、B三点,A(4,0)B(1,-3),P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)直线PQ与x轴所夹锐角的度数,并求出抛物线的解析式.
(2)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求: PD+DQ的最大值;②PD.DQ的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com