
【题目】如图1,在平面直角坐标系![]() 中,点A的坐标是
中,点A的坐标是![]() ,点C是x轴上的一个动点.当点C在x轴上移动时,始终保持
,点C是x轴上的一个动点.当点C在x轴上移动时,始终保持![]() 是等腰直角三角形(
是等腰直角三角形(![]() ,点A、C、P按逆时针方向排列);当点C移动到点O时,得到等腰直角三角形
,点A、C、P按逆时针方向排列);当点C移动到点O时,得到等腰直角三角形![]() (此时点P与点B重合).
(此时点P与点B重合).
(初步探究)
(1)写出点B的坐标________;
(2)点C在x轴上移动过程中,作![]() 轴,垂足为点D,都有
轴,垂足为点D,都有![]() ,请在图2中画出当等腰直角
,请在图2中画出当等腰直角![]() 的顶点P在第四象限时的图形,并求证:
的顶点P在第四象限时的图形,并求证:![]() .
.
(深入探究)
(3)当点C在x轴上移动时,点P也随之运动.探究点P在怎样的图形上运动,请直接写出结论,并求出这个图形所对应的函数表达式;
(4)直接写出![]() 的最小值为________.
的最小值为________.



【答案】(1)![]() ;(2)证明见解析;(3)点P在直线上运动;
;(2)证明见解析;(3)点P在直线上运动;![]() ;(4)8.
;(4)8.
【解析】
(1)根据等腰三角形的性质即可求解;
(2)根据题意作图,再根据等腰直角三角形的性质判定![]() ;
;
(3)根据题意去特殊点,再利用待定系数法即可求解;
(4)当P在B点时,AP最小,故可求解.
(1)∵点A的坐标是![]() ,△
,△![]() 为等腰直角三角形,
为等腰直角三角形,
∴AO=BO
∴![]()
(2)如图,
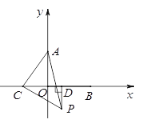
∵![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ∴
∴![]()
∵![]() ∴
∴![]() ∴
∴![]() ,
,![]()
∵![]() ∴
∴![]() ∴
∴![]()
在![]() 和
和![]() 中,
中,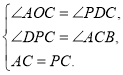 ∴
∴![]()
(3)点P在直线上运动;
∵两点确定一条直线
∴可以取两个特殊点
当P在y轴上时,![]() ,
,
∴![]()
当P在x轴上时,![]() ,∴
,∴![]()
设所求函数关系式为![]() ;
;
将![]() 和
和![]() 代入,得
代入,得![]()
![]() 解得
解得![]()
![]()
所以所求的函数表达式为![]() ;
;
(4)如图,作AP⊥直线![]() ,即P与B点重合,
,即P与B点重合,
∴AP2=22+22=8.


科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠海到韶关的距离约为360千米,小刘驾驶小轿车,小张驾驶大货车,两人都从珠海去韶关,小刘比小张晚出发90分钟,最后两车同时到达韶关,已知小轿车的速度是大货车速度的1.5倍.
(1)分别求小轿车和大货车的速度;
(2)当小刘行驶了2小时,此时两车相距多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在三角形![]() 中,把
中,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(特例尝试)如图2,当![]() 时,
时,
①求证:![]() ;
;
②猜想![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
(理想论证)在图1中,当![]() 为任意三角形时,②中
为任意三角形时,②中![]() 与
与![]() 的数量关系还成立吗?请给予证明.
的数量关系还成立吗?请给予证明.
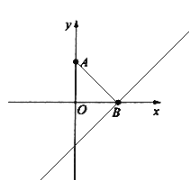
(拓展应用)如图3,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,分别以
两点,分别以![]() ,
,![]() 为直角边在第二、一象限内作等腰
为直角边在第二、一象限内作等腰![]() 和等腰
和等腰![]() ,连接
,连接![]() ,交
,交![]() 轴于点
轴于点![]() .试猜想
.试猜想![]() 的长是否为定值,若是,请求出这个值;若不是,请说明理由.
的长是否为定值,若是,请求出这个值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图像与y轴交于点A,一次函数
的图像与y轴交于点A,一次函数![]() 的图像经过点
的图像经过点![]() ,与x轴交于点C,与
,与x轴交于点C,与![]() 的图像交于点D,且点D的坐标为
的图像交于点D,且点D的坐标为![]() .
.
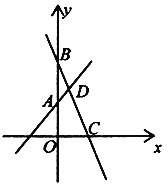
(1)求k和b的值;
(2)若![]() ,则x的取值范围是__________.
,则x的取值范围是__________.
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.

(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为x厘米/秒,则当△BPD与△CQP全等时,x的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,每个小正方形的边长为1个单位长度.
(1)作出△ABC关于原点对称的△A1B1C1,并写出A1,B1,C1的坐标.
(2)y轴上有一点Q,使AQ+CQ的值最小,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标第中有一个2×2的正方形网格,每个格点的横、纵坐标均为整数,已知点A(1,2).作直线OA并向右平移k个单位,要使分布在平移后的直线两侧的格点数相同,则k的值为( )
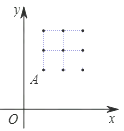
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com