
【题目】为提醒人们节约用水,及时修好漏水的水龙头.小明同学做了水龙头漏水实验,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升),已知用于接水的量筒最大容量为100毫升.
时间t(秒) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
量筒内水量v(毫升) | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
(1)在图中的平面直角坐标系中,以(t,v)为坐标描出上表中数据对应的点;
(2)用光滑的曲线连接各点,你猜测V与t的函数关系式是______________.
(3)解决问题:
①小明同学所用量筒开始实验前原有存水 毫升;
②如果小明同学继续实验,当量筒中的水刚好盛满时,所需时间是_____秒;
③按此漏水速度,半小时会漏水 毫升.
科目:初中数学 来源: 题型:
【题目】为了了解居民的环保意识,社区工作人员在某小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖答卷活动(每名居民必须答卷且只答一份),并用得到的数据绘制了如图所示的条形统计图(得分为整数,满分为![]() 分,最低分为
分,最低分为![]() 分)
分)
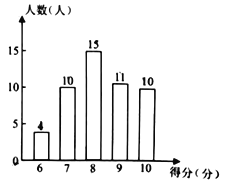
请根据图中信息,解答下列问题:
(1)本次调查,一共抽取了多少名居民?
(2)求本次调查获取的样本数据的平均数和众数;
(3)社区决定对该小区![]() 名居民开展这项有奖答卷活动,得
名居民开展这项有奖答卷活动,得![]() 分者获一等奖,请你根据调查结果,帮社区工作人员估计需要准备多少份一等奖奖品?
分者获一等奖,请你根据调查结果,帮社区工作人员估计需要准备多少份一等奖奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元;购买
元;购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元.
元.
(1)求购买一个甲种文具、一个乙种文具各需多少元?
(2)若学校计划购买这两种文具共![]() 个,投入资金不少于
个,投入资金不少于![]() 元又不多于
元又不多于![]() 元,设购买甲种文具
元,设购买甲种文具![]() 个,求有多少种购买方案?
个,求有多少种购买方案?
(3)设学校投入资金![]() 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:数学兴趣一小组的同学对完全平方公式进行研究:因![]() ,将左边展开得到
,将左边展开得到![]() ,移项可得:
,移项可得:![]() .
.
数学兴趣二小组受兴趣一小组的启示,继续研究发现:对于任意两个非负数![]() 、
、![]() ,都存在
,都存在![]() ,并进一步发现,两个非负数
,并进一步发现,两个非负数![]() 、
、![]() 的和一定存在着一个最小值.
的和一定存在着一个最小值.
根据材料,解答下列问题:
(1)![]() __________(
__________(![]() ,
,![]() );
);![]() ___________(
___________(![]() );
);
(2)求![]() 的最小值;
的最小值;
(3)已知![]() ,当
,当![]() 为何值时,代数式
为何值时,代数式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2)点M是边BC上的一个动点(不与B、C重合),反比例函数![]() (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
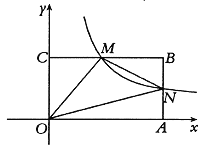
(1)当点M是边BC的中点时,求反比例函数的表达式;
(2)在点M的运动过程中,试证明:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
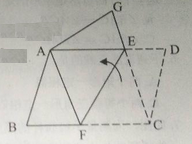
【题目】如图,将一张平行四边形纸片ABCD沿着线段EF折叠(点E、F分别在AB边和BC边上),使得点C落在点A处,点D落在点G出。
(1)如果连接EC,那么线段GE与EC在同一条直线上吗?为什么?
(2)试判断四边形AFCE的形状,并说明你是怎样判断的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店销售一批衬衫,每件进价![]() 元,开始以每件
元,开始以每件![]() 元的价格销售,每星期能卖出
元的价格销售,每星期能卖出![]() 件,后来因库存积压,决定降价销售,经两次降价后的每件售价
件,后来因库存积压,决定降价销售,经两次降价后的每件售价![]() 元,每星期能卖出
元,每星期能卖出![]() 件.
件.
![]() 已知两次降价百分率相同,求每次降价的百分率;
已知两次降价百分率相同,求每次降价的百分率;
![]() 聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低
聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低![]() 元,销售会增加
元,销售会增加![]() 件,若店主想要每星期获利
件,若店主想要每星期获利![]() 元,应把售价定为多少元?
元,应把售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y1=mx2﹣4mx+2n﹣1与平行于x轴的直线交于A、B两点,且A点坐标为(﹣1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,﹣1);③m>![]() ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是
;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是![]() ≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
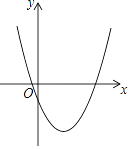
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 、
、![]() 分别与圆相交于
分别与圆相交于![]() 、
、![]() ,那么下列等式中一定成立的是( )
,那么下列等式中一定成立的是( )
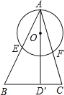
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com