
分析 由题意得:a={a}+[a],即一个实数a=a的整数部分+a的小数部分,将三个等式相加得:x+y+z=0.3④,依次与三个等式相减得到x、y、z的值,代入可求得结果.
解答 解:∵{a}=a-[a],
∴a={a}+[a],
∵$\left\{\begin{array}{l}{x+[y]+\{z\}=-0.9①}\\{[x]+\{y\}+z=0.2②}\\{\{x\}+y+[z]=1.3③}\end{array}\right.$
①+②+③得:x+[x]+{x}+y+[y]+{y}+z+[z]+{z}=0.6,
2x+2y+2z=0.6,
x+y+z=0.3④,
④-①得:{y}+[z]=1.2,所以{y}=0.2,[z]=1,
④-②得:{x}+[y]=0.1,所以[y]=0,{x}=0.1,
④-③得:[x]+{z}=-1,所以{z}=0,[x]=-1,
∴x=[x]+{x}=-1+0.1=-0.9,y=[y]+{y}=0+0.2=0.2,z=[z]+{z}=1+0=1,
∴10(x+y)+z=10×(-0.9+0.2)+1=-6.
点评 此题考查了取整函数的应用,知道不超过实数a的最大整数称为a的整数部分,记作[a]. a-[a]称为x的小数部分,记作{a};解题时要注意[a]=a-{a}的应用,并注意等式之间的加减变形.


科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
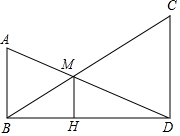 如图,AB和CD表示两根立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知AB=10m,CD=15m,则点M离地面的高度MH=6m.
如图,AB和CD表示两根立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知AB=10m,CD=15m,则点M离地面的高度MH=6m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB,CB⊥AB,已知DA=15km,CB=10km.
如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB,CB⊥AB,已知DA=15km,CB=10km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com